Как найти коэффициент корреляции в Excel
К чему этот материал
Детализированное руководство для специалистов, которым нужно: вычислить корреляцию в Excel, визуализировать связи, сравнить методы (CORREL, PEARSON, ToolPak), и понимать, когда корреляция вводит в заблуждение. Подходит аналитикам, менеджерам и исследователям, работающим с табличными данными.
Что такое корреляция
Корреляция — это статистическое измерение того, насколько две переменные связаны линейно. Корреляция не говорит о причинно‑следственной связи — она лишь показывает степень и направление линейной зависимости.
- Значение коэффициента лежит в диапазоне от −1 до +1.
- +1: идеальная прямая положительная зависимость (по мере роста X растёт Y пропорционально).
- −1: идеальная обратная зависимость (по мере роста X Y уменьшается пропорционально).
- 0: отсутствует линейная связь; переменные могут быть нерелевантными или связаны нелинейно.

ALT: График двух случайных наборов данных, демонстрирующий отсутствие линейной связи
Когда корреляция может ввести в заблуждение — кратко
- Нелинейные связи могут давать коэффициент, близкий к нулю.
- Сильные выбросы и тренды во временных рядах искажают значение.
- Общие факторы (конфайндинг) и автокорреляция во временных данных создают ложную значимость.
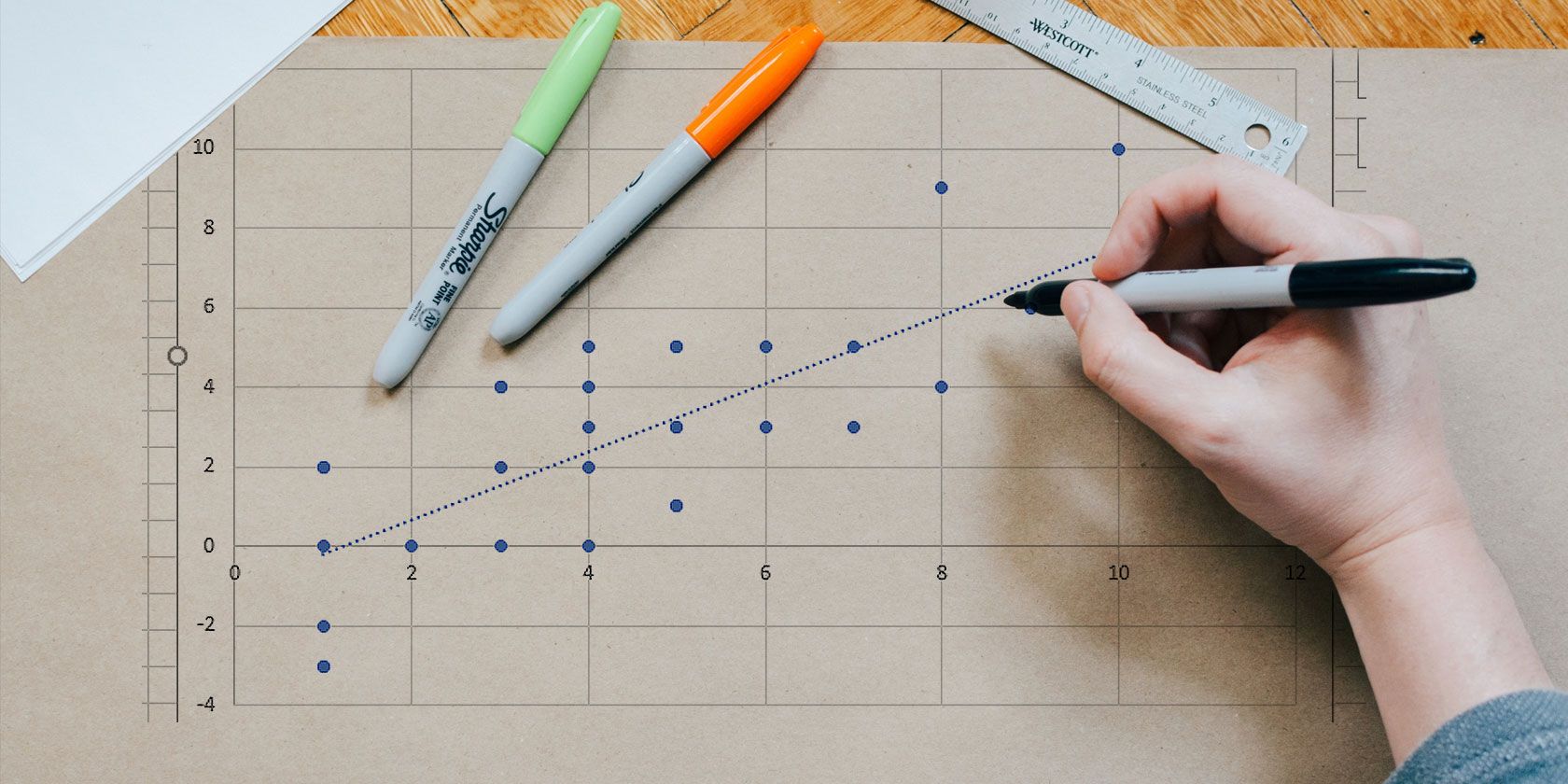
ALT: Точечный график, показывающий отсутствие шаблона и отсутствие корреляции между X и Y
ALT: Точечный график с явно выраженной положительной линейной зависимостью между двумя переменными
Коэффициент корреляции — что он показывает
Коэффициент корреляции Пирсона (наиболее распространённый) измеряет линейную зависимость. Он чувствителен к выбросам и предполагает, что переменные приблизительно нормально распределены, если вы собираетесь делать выводы о значимости.
- Примеры интерпретации (правило большого пальца):
- |r| < 0.1 — практически нет связи
- 0.1 ≤ |r| < 0.3 — слабая связь
- 0.3 ≤ |r| < 0.5 — умеренная связь
- |r| ≥ 0.5 — сильная связь
Замечание: эти границы условны и зависят от предметной области.
ALT: Пример нелинейной связи (парабола): при сильной зависимости коэффициент Пирсона близок к нулю
Как найти коэффициент корреляции в Excel с помощью CORREL
В Excel есть встроенная функция для расчёта корреляции:
=CORREL(array1, array2)array1 — первая серия данных, array2 — вторая. Функция возвращает числовое значение r.
Пример использования:
- Подготовьте данные в двух столбцах (не должно быть пустых строк внутри выбранных диапазонов).
- Введите формулу, например: =CORREL(A2:A101,B2:B101).
- Нажмите Enter — вы получите коэффициент корреляции.
ALT: Фрагмент Excel‑таблицы с формулой CORREL, показан результат слабой положительной связи между годом модели и ценой
Дополнительные формулы, полезные в Excel:
- =PEARSON(array1,array2) — эквивалент CORREL (в старых версиях Excel использовался PEARSON).
- =RSQ(Y_range,X_range) — возвращает R^2 (коэффициент детерминации) для линейной зависимости.
- =SLOPE(Y_range,X_range), =INTERCEPT(Y_range,X_range), =LINEST(…) — для параметров линейной регрессии.
Графики: как визуализировать корреляцию
Визуальная проверка связей обязательна перед тем, как доверять числу корреляции.
- Постройте диаграмму рассеяния (scatter): Вкладка «Вставка» → «Диаграммы» → «Точечная (Scatter)».
- Добавьте линию тренда (trendline) и при необходимости покажите уравнение и R‑квадрат.
- Проверяйте на предмет выбросов, нелинейных паттернов и неоднородности дисперсий.
ALT: Диаграмма рассеяния в Excel с заметной, но слабой положительной тенденцией
Добавление линии тренда (в десктопных версиях Excel): выделите диаграмму → контекстная вкладка «Конструктор» или «Макет диаграммы» → «Добавить элемент диаграммы» → «Линия тренда» → «Линейная». Можно включить отображение уравнения и R^2.
ALT: Диаграмма рассеяния с добавленной линейной линией тренда и уравнением регрессии
Корреляция между множеством переменных — Data Analysis ToolPak
Для матрицы корреляций нескольких столбцов удобнее использовать «Набор средств анализа» (Analysis ToolPak).
- Убедитесь, что надстройка установлена (Файл → Параметры → Надстройки → Управление: Надстройки Excel → Перейти → ставим галочку Analysis ToolPak).
- Вкладка «Данные» → «Анализ данных» → выберите «Корреляция» → укажите Input Range (включая заголовки, если нужно) и Output Range.
- Excel вернёт матрицу корреляций: каждая диагональная ячейка будет равна 1.
ALT: Окно «Анализ данных» в Excel с выделенной опцией Correlation
ALT: Окно настройки диапазона входных данных и места вывода результатов корреляции
ALT: Пример выходной матрицы корреляций, демонстрирующей сильную корреляцию между годом и населением и слабую между случайными столбцами
Корреляция и линейная регрессия — отличия и связь
Корреляция измеряет силу линейной связи между двумя переменными. Линейная регрессия моделирует зависимость Y от X и позволяет делать предсказания и тесты гипотез о значимости.
- Регрессия даёт коэффициенты (наклон, пересечение), стандартные ошибки, p‑значения и R^2.
- Корреляция — простое и быстрое число r.
- Нулевая корреляция не исключает нелинейной зависимости; низкое p‑значение в регрессии говорит о статистической значимости, но не о причинности.
Пример: запустите «Regression» в Data Analysis ToolPak, укажите Input Y Range и Input X Range, выберите Output Range. В таблице регрессии обратите внимание на p‑value для коэффициентов (обычно порог 0.05 для типичных исследований).
ALT: Окно настройки регрессии в Excel с полями для диапазонов X и Y
ALT: Результат регрессии в Excel с ключевыми статистиками: коэффициенты, стандартные ошибки, p‑значения и R‑квадрат
Важные оговорки по регрессии
- p‑value < 0.05 говорит о статистической значимости, но не о причинности.
- Мультиколлинеарность (сильные корреляции между X‑переменными) затрудняет интерпретацию коэффициентов.
ALT: Результат множественной регрессии в Excel с двумя объясняющими переменными и их p‑значениями
Когда корреляция «не работает» — конкретные сценарии
- Нелинейная зависимость (например, квадратичная): r может быть близким к 0.
- Временные ряды с трендами: два независимых тренда могут показать высокую корреляцию.
- Наличие одного или нескольких выбросов: они могут полностью изменить r.
- Смешивание разных популяций в одном наборе данных (спрямление): внутрипопуляционная связь исчезает.
Руководство: всегда строите диаграммы и проверяйте распределение, тренды и выбросы.
Альтернативные подходы и устойчивые меры
- Коэффициент Спирмена (Spearman) — ранговая корреляция, устойчива к нелинейным монотонным связям и некоторым выбросам (в Excel можно вычислить ранги функцией RANK.AVG и затем CORREL по рангам).
- Кендалла (Kendall) — ещё одна ранговая мера, статистически более точная при малых выборках.
- Частичная корреляция — удаляет эффект одной или нескольких контролируемых переменных.
- Robust correlation (робастные методы) — например, основанные на медиане и бипертусе; в Excel это обычно требует доп. инструментов или скриптов.
Как быстро вычислить корреляцию Спирмена в Excel (мини‑инструкция)
- Для каждой серии данных создайте колонки с рангами: =RANK.AVG(A2,$A$2:$A$101,1) (или 0 в третьем аргументе в зависимости от сортировки).
- Примените =CORREL(RankX_range,RankY_range).
Сравнительная таблица: CORREL vs PEARSON vs ToolPak vs Spearman
| Метод | Что возвращает | Устойчивость к выбросам | Подходит для | Нужны дополнительные шаги |
|---|---|---|---|---|
| CORREL | r (Пирсон) | Низкая | Линейная связь | Нет |
| PEARSON | r (аналог CORREL) | Низкая | Линейная связь | Нет |
| Data Analysis ToolPak — Correlation | Матрица r | Низкая | Много столбцов | Нет |
| Spearman (через ранги) | Ранговая r | Высокая | Монотонные или с выбросами | Нужно создать ранги |
Практическая методология: пошаговый SOP для анализа корреляции в Excel
- Определите цель: описательная оценка или тест гипотезы?
- Подготовьте данные: удалите/обработайте пропуски, проверьте одинаковое количество наблюдений.
- Визуализируйте данные: scatter plot, гистограммы, boxplot (если много выбросов).
- Проверьте предпосылки: линейность, распределение, гомоскедастичность, выбросы.
- Выберите меру: Pирсон для линейных, Спирмен для ранговых/много выбросов.
- Вычислите корреляцию: CORREL или через ToolPak для матриц.
- Интерпретируйте: сила, направление, практическая значимость.
- При необходимости примените регрессию и тесты значимости.
- Документируйте шаги, диапазоны и версии файлов/таблиц.
Контрольные тест‑кейсы (кратко)
- Тест 1: Два независимых нормальных набора → r ≈ 0.
- Тест 2: Явная линейная зависимость (Y=2X+noise) → r высокий и положительный.
- Тест 3: Нелинейная зависимость (парабола) → r близок к 0, но визуализация показывает связь.
- Тест 4: Добавление одного сильного выброса → r значительно изменяется.
Чеклисты по ролям
Аналитик:
- Проверить пропуски и соответствие размеров массивов.
- Построить scatter plot и линию тренда.
- Рассчитать CORREL и R^2.
- Запустить регрессию при необходимости.
Менеджер/решающий:
- Попросить визуализации и интерпретацию практического эффекта.
- Уточнить возможные конфаундеры и логику причинности.
Исследователь:
- Проверить устойчивые меры (Spearman), частичную корреляцию.
- Документировать предположения и ограничения анализа.
Шаблон отчёта (короткий)
- Цель анализа: …
- Данные: источники, периоды, размер выборки.
- Подготовка: удаление пропусков, трансформации.
- Методы: CORREL / Spearman / регрессия.
- Результат: r = …, R^2 = …, p‑value = …
- Визуализация: прикреплён scatter plot с линией тренда.
- Ограничения: перечислите 2–3 ключевых.
Ментальная модель: как думать о корреляции
- Корреляция — это мера «как близко точки находятся к прямой».
- Корреляция не отвечает на вопрос «почему».
- Визуализация — первичный инструмент контроля качества результата.
Мерчантайзинг Excel‑приёмов: полезные формулы и сниппеты
- CORREL: =CORREL(A2:A101,B2:B101)
- PEARSON: =PEARSON(A2:A101,B2:B101)
- R^2 через формулу: =RSQ(A2:A101,B2:B101)
- SLOPE/INTERCEPT: =SLOPE(Y_range,X_range), =INTERCEPT(Y_range,X_range)
- RANK.AVG: =RANK.AVG(A2,$A$2:$A$101,1) — для рангов Спирмена
- LINEST (массив): =LINEST(Y_range,X_range,TRUE,TRUE) — аккуратно, возвращает массивы; вводить как формулу массива в старых Excel
Небольшая проверка качества: критерии приёмки
- Диапазон без пустых строк в выбранных диапазонах.
- Визуальная диаграмма рассеяния приложена.
- Формулы задокументированы и легко воспроизводимы.
- Для выводов по значимости приложены результаты регрессии или ранговых тестов.
Риск‑матрица: возможные ошибки и смягчения
- Риск: Нелинейная зависимость → Смягчение: используйте Спирмена/постройте график.
- Риск: Выбросы → Смягчение: удалить/проверить влияние, использовать ранговые методы.
- Риск: Тренды в временных рядах → Смягчение: детрендирование или разности.
Краткий глоссарий (1‑строчные определения)
- Корреляция: мера линейной связи между двумя переменными.
- r: коэффициент корреляции Пирсона.
- R^2: доля дисперсии Y, объясняемая X в линейной модели.
- p‑value: вероятность наблюдения таких данных при нулевой гипотезе (обычно p<0.05 считается статистически значимым).
Быстрый справочник: когда выбирать метод
- Нужна простая оценка линейной связи → CORREL/PEARSON.
- Есть выбросы или монотонная связь → Spearman (по рангам).
- Много переменных → Correlation через ToolPak.
- Нужна причинная интерпретация или предсказание → Регрессия + контроль переменных.
Пример сценария и решение (коротко)
Задача: проверить, влияет ли год выпуска автомобиля на его цену. Шаги: очистка данных → scatter plot → CORREL(year,price) → регрессия price~year → проверить p‑value и R^2 → оценить практическое значение (насколько меняется цена при увеличении года на 1 год).
Итог и рекомендации
Корреляция в Excel — быстрый и полезный инструмент для первичной оценки линейных связей. Всегда сопровождайте численные результаты визуализациями и думайте о возможных альтернативных объяснениях. При необходимости переходите к регрессии и проверяйте предпосылки статистических тестов.
Важно: корреляция — это измерение связи, а не доказательство причинности. Документируйте все шаги и храните исходные диапазоны и версии файлов.
Есть ли у вас конкретный набор данных, с которым вы хотите, чтобы я показал пример пошагово (на уровне формул и диаграмм)?
Похожие материалы

RDP: полный гид по настройке и безопасности

Android как клавиатура и трекпад для Windows

Советы и приёмы для работы с PDF

Calibration в Lightroom Classic: как и когда использовать

Отключить Siri Suggestions на iPhone
