Число Армстронга: алгоритм и пример на C

Экран ноутбука с кодом

Что такое число Армстронга?

Число Армстронга (в простом трёхзначном варианте) — это такое число, сумма кубов его цифр равна самому числу. Пример: 153 — число Армстронга, потому что:

(1 × 1 × 1) + (5 × 5 × 5) + (3 × 3 × 3) = 1 + 125 + 27 = 153.

Важно: в общем определении степень, в которую возводят каждую цифру, равна количеству цифр числа. Для трёхзначных чисел это куб; для четырёхзначных — четвёртая степень и т. д. В этой статье мы подробно разберём вариант с суммой кубов (как в исходном примере), укажем обобщение и приведём советы по реализации.

Алгоритм для проверки числа на Армстронга

Общая идея проста и часто используется при работе с цифрами числа:

Инициализировать sum = 0 и сохранить копию исходного числа temp = n.
Пока n > 0:
- r = n % 10 — получить последнюю цифру.
- sum = sum + (r r r) — добавить куб цифры (для трёхзначного определения).
- n = n / 10 — отбросить последнюю цифру (целочисленное деление).
Если sum == temp — число Армстронга, иначе — нет.

Пошаговый псевдокод и идеи полезны при переводе алгоритма в любой язык программирования.

Псевдокод реализации

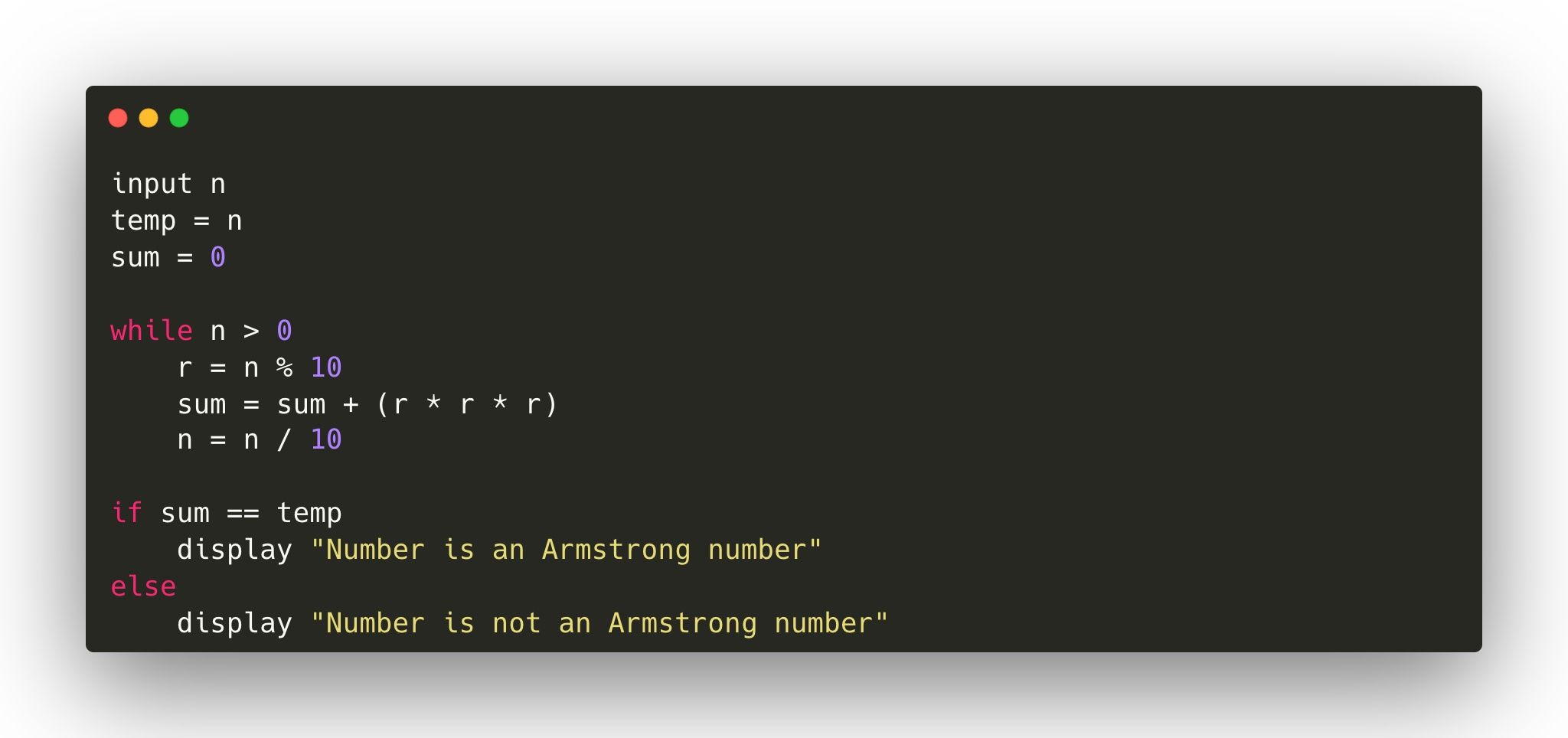
Схема алгоритма для проверки числа на Армстронга

Псевдокод помогает спроектировать программу перед написанием кода. Ниже — компактный псевдокод, соответствующий описанному алгоритму:

Ввод: целое число n
sum = 0; temp = n
Пока n > 0:
- r = n % 10
- sum = sum + (r r r)
- n = n / 10
Если sum == temp: вывести, что число Армстронга
Иначе: вывести, что не Армстронга

Программа на C (пошагово)

Ниже — исходный пример на C, в точности как в типичных учебных материалах. Код требует заголовка stdio.h для ввода/вывода. Переменные: n — входное число, r — текущая цифра, sum — сумма кубов цифр, temp — копия исходного числа.

#include   
  
int main()  
{  
    int n, r, sum, temp;  
    printf("Please enter a number: ");  
    scanf("%d", &n);  
    sum = 0; temp = n;

Далее — цикл, который извлекает цифры и накапливает сумму кубов:

    while (n > 0) {  
        r = n % 10;  
        sum = sum + (r * r * r);  
        n = n / 10;  
    }

Проверка результата и завершение программы:

    if (temp == sum)  
        printf("Number is an Armstrong number\n");  
    else  
        printf("Number is not an Armstrong number\n");  
  
    return 0;  
}

Примечание: строки ввода/вывода в примере на английском оставлены без изменений. Код корректно работает для положительных целых чисел.

Почему этот метод работает: разбор приёмов по цифрам

Обработка цифр через остаток и целочисленное деление — базовый приём:

n % 10 даёт последнюю цифру r.
n = n / 10 удаляет последнюю цифру.
Операции повторяются до тех пор, пока не обработаны все цифры.

Этот трёхшаговый приём (извлечение цифры, операция над цифрой, удаление цифры) применим во множестве задач с числами — суммирование цифр, произведение цифр, подсчёт цифр, реверс числа и т. д.

Альтернативные подходы к реализации

Строковый метод. Преобразуйте число в строку, пройдитесь по символам, преобразуйте каждый символ в цифру и возведите в степень. Подходит для языков с удобными операциями со строками.
Использование pow() из math.h. Вместо (rrr) можно написать pow(r, k), где k — степень (число цифр). Минус: pow возвращает double — нужно аккуратно округлять и работать с целыми типами.
Рекурсивная версия. Реализуйте рекурсивный проход по цифрам, накапливая сумму. Подходит для демонстрации рекурсии, но менее эффективна по стеку.
Предкомпиляция степеней. Если вы проверяете множество чисел, можно заранее вычислить таблицу power[digit][k] для ускорения.

Общая формулировка и ограничения

Обобщённое определение: число n с d цифрами называется числом Армстронга, если сумма d‑й степени его цифр равна n. Для трёхзначных чисел это эквивалент суммы кубов.

Ограничения практики:

Для больших чисел нужно учитывать переполнение целочисленных типов.
Для использования pow() учитывайте погрешности плавающей точки.
Ноль и однозначные числа технически являются числами Армстронга по общей формуле (каждая цифра^1 равна самой цифре).

Примеры чисел Армстронга

153 — 1^3 + 5^3 + 3^3 = 153
370 — 3^3 + 7^3 + 0^3 = 370
371 — 3^3 + 7^3 + 1^3 = 371
407 — 4^3 + 0^3 + 7^3 = 407

Эти четыре числа — общепринятые примеры трёхзначных чисел Армстронга.

Критерии приёмки (тесты и входные данные)

Рекомендуемые тесты для проверки корректности реализации:

Ввод: 153 → ожидаемый вывод: число Армстронга
Ввод: 370 → ожидаемый вывод: число Армстронга
Ввод: 371 → ожидаемый вывод: число Армстронга
Ввод: 407 → ожидаемый вывод: число Армстронга
Ввод: 0 → ожидаемый вывод: число Армстронга (по общему определению)
Ввод: 1 → ожидаемый вывод: число Армстронга
Ввод: 9474 → в трёхзначной версии — не Армстронга; в обобщённой версии (4‑я степень) — Армстронга
Отрицательные числа: определитесь с политикой — обычно рассматривают только неотрицательные числа

Критерии приёмки кода:

Корректно обрабатывает все неотрицательные целые входы в допустимом диапазоне типа int.
Не использует лишнюю память и имеет сложность O(d), где d — число цифр.
Работает без ошибок при стандартном вводе.

Тестовые случаи и граничные условия

Очень большие числа (проверить переполнение sum). Решение: использовать шире тип (long long) или ограничить вход.
Числа с ведущими нулями: в числовом вводе ведущие нули исчезают.
Использование pow(r, d) может дать нецелые значения из‑за double; при сравнении применяйте безопасное округление.

Когда этот метод не подходит (контрпримеры)

Задачи, где степень зависит от количества цифр: если код жёстко считает куб, он неправильно определит числа с другой длиной (например, 9474). Нужно вычислять d = количество цифр и использовать r^d.
Очень большие числа, где сумма степеней превышает диапазон целого типа.

Оптимизации и эвристики (ментальные модели)

Эвристика проверки диапазона: для числа с d цифрами максимальная возможная сумма d раз 9^d. Если это меньше минимального d-значного числа (10^{d-1}), то дальнейшие проверки для таких d бессмысленны.
Предкомпиляция значений степеней 0..9 для каждой возможной d ускоряет многократные проверочные прогонки.

Роль‑ориентированные чеклисты

Для студента:

Понимаю механизм % и / для выделения цифр.
Могу реализовать цикл извлечения цифр.
Покрыл тестами 153, 370, 371, 407, 0.

Для разработчика:

Проверил переполнение и типы.
Добавил обработку отрицательных входов или явно запретил их.
Добавил юнит‑тесты и документировал ограничения.

Для ревьюера:

Код прост и читабелен.
Некорректное использование pow() отсутствует или безопасно обёрнуто.
Есть тесты на граничные случаи и описание предпосылок.

Мини‑методология внедрения

Реализовать простую версию с (rrr) для учебных задач.
Написать набор unit‑тестов (см. критерии приёмки).
При необходимости обобщить до степени d и заменить выражение (rrr) на предвычисленные таблицы степеней.
Проверить поведение при больших входах и выбрать тип для суммирования (long long или bigint).

Примерный план миграции на обобщённую версию (если нужно)

Шаг 1: написать функцию count_digits(n).
Шаг 2: вычислить d = count_digits(n).
Шаг 3: для каждой цифры r добавить pow(r, d) (предпочтительно через lookup table).

Mermaid‑диаграмма алгоритма (flowchart):

flowchart TD
  A[Начало] --> B{n > 0?}
  B -- Да --> C[r = n % 10]
  C --> D[sum += r^k]
  D --> E[n = n / 10]
  E --> B
  B -- Нет --> F{sum == temp?}
  F -- Да --> G[Вывести: Армстронг]
  F -- Нет --> H[Вывести: Не Армстронг]
  G --> I[Конец]
  H --> I

Примечания по локализации и учебному использованию

При переводе учебных примеров на другие языки программирования сохраняйте шаги: извлечение цифры, операция, удаление цифры.
Для демонстрации алгоритма оставляйте простые значения и понятные тесты.

Важно: не меняйте исходную логику в учебных примерах без ясной причины. Если нужна общая версия — явно укажите, что вы обобщаете степень до числа цифр.

Краткое резюме

Число Армстронга проверяют суммированием степеней цифр.
Для трёхзначных чисел используют сумму кубов цифр.
Метод основан на % и / и имеет сложность O(d), где d — число цифр.
При переходе к большим числам учтите переполнение и точность pow().

Если нужно, могу:

предоставить готовую обобщённую реализацию на C (с подсчётом цифр и предвычислением степеней),
добавить unit‑тесты в формате для вашей тестовой среды,
или привести реализацию на другом языке (Python, Java, JavaScript).