Как умножать матрицы — понятное руководство

Матрицы используются в графике, криптографии, обработке сигналов, анализе данных и многих других областях. Матрица — это прямоугольная таблица чисел, упорядоченных в строки и столбцы. Умножение матриц позволяет представлять композиции преобразований, решать системы линейных уравнений и описывать линейные отображения.

Что нужно знать перед началом

• Определение: матрица m×n имеет m строк и n столбцов. Кратко: m × n.
• Условие совместимости: если A размером m×n и B размером n×p, то A×B определено и имеет размер m×p.
• Термин: скалярное произведение (dot product) — сумма попарных произведений элементов двух векторов одинаковой длины.

Краткие определения:

• Строка — горизонтальный вектор.
• Столбец — вертикальный вектор.

Как умножать две матрицы — пошаговый пример

Пусть

A = [[1, 2, 3],

 [4, 5, 6]]  (размер 2×3)

B = [[7, 8],

 [9, 10],
 [11, 12]]    (размер 3×2)

Поскольку число столбцов A (3) равно числу строк B (3), умножение возможно. Результат будет матрица размера 2×2.

Вычисляем элементы результата C = A × B:

• C[0][0] = (1,2,3) · (7,9,11) = 1×7 + 2×9 + 3×11 = 58
• C[0][1] = (1,2,3) · (8,10,12) = 1×8 + 2×10 + 3×12 = 64
• C[1][0] = (4,5,6) · (7,9,11) = 4×7 + 5×9 + 6×11 = 139
• C[1][1] = (4,5,6) · (8,10,12) = 4×8 + 5×10 + 6×12 = 154

Итого:

C = [[58, 64],

 [139,154]]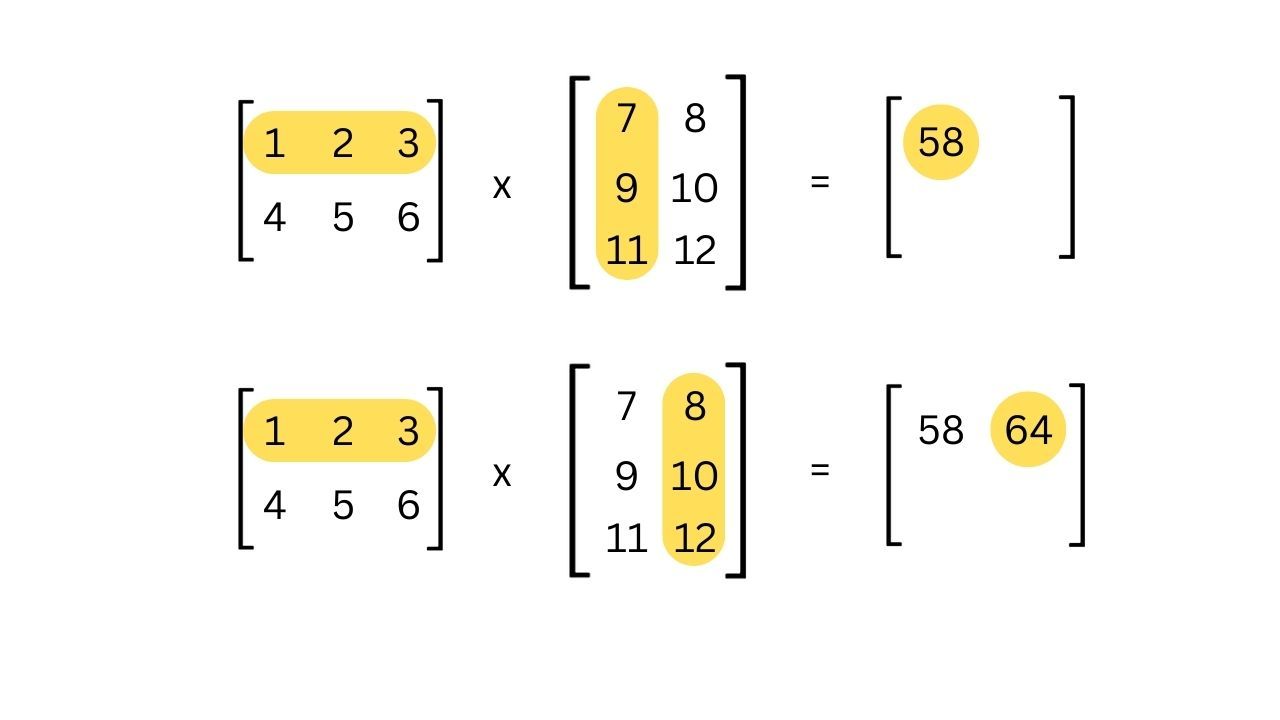

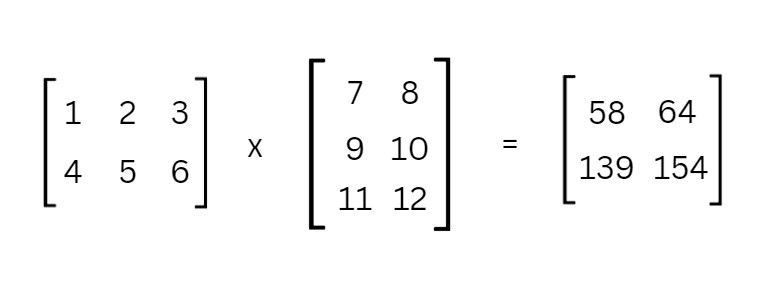
Алгоритм умножения матриц (пошагово)

1. Начать программу.
2. Прочитать число строк и столбцов первой матрицы (r1, c1).
3. Прочитать число строк и столбцов второй матрицы (r2, c2).
4. Если c1 != r2 — вывести ошибку и завершить.
5. Ввести элементы первой матрицы m1[r1][c1].
6. Ввести элементы второй матрицы m2[r2][c2].
7. Инициализировать матрицу результата mul[r1][c2] нулями.
8. Для i от 0 до r1-1:
   • Для j от 0 до c2-1:
     • Для k от 0 до c1-1:
       • mul[i][j] += m1[i][k] * m2[k][j]
9. Вывести матрицу mul.
10. Завершить программу.

Ключевой шаг — внутренний цикл k, который реализует скалярное произведение строки и столбца.

Реализация на C — разбор примера

Ниже приведён полный фрагмент кода на C, как он встречался в исходном материале. Код использует ввод через scanf и динамику размеров через VLA (variable length arrays).

#include   
#include   
  
int main()  
{  
    int r1, r2, c1, c2;  
  
    printf("Enter the number of rows for the first matrix:\n");      
    scanf("%d", &r1);      
  
    printf("Enter the number of columns for the first matrix:\n");       
    scanf("%d", &c1);   
  
    printf("Enter the number of rows for the second matrix:\n");      
    scanf("%d", &r2);      
  
    printf("Enter the number of columns for the second matrix:\n");       
    scanf("%d", &c2);

Проверка совместимости:

    if (c1 != r2) {  
        printf("The matrices cannot be multiplied together");  
       exit(-1);  
    }

Ввод элементов и вычисление:

    int m1[r1][c1], m2[r2][c2];  
    printf("Enter the elements of the first matrix\n");  
  
    for (int i = 0; i < r1; i++) {      
        for (int j = 0; j < c1; j++) {      
            scanf("%d", &m1[i][j]);  
        }      
    }      
  
    printf("Enter the elements of the second matrix\n");      
  
    for (int i = 0; i < r2; i++) {      
        for (int j = 0; j < c2; j++) {  
            scanf("%d",&m2[i][j]);      
        }      
    }    

Вычисление результата:

    int mul[r1][c2];  
  
    for (int i = 0; i < r1; i++) {      
        for (int j = 0; j < c2; j++) {      
            mul[i][j] = 0;  
  
            for (int k = 0; k < c1; k++) {  
                mul[i][j] += m1[i][k] * m2[k][j];      
            }   
        }      
    }   

Вывод:

    printf("The multiplied matrix is: \n");       
  
    for (int i = 0; i < r1; i++) {      
        for (int j = 0; j < c2; j++) {  
            printf("%d\t", mul[i][j]);  
        }      
  
        printf("\n");  
    }  
  
    return 0;    
}

Пример вывода программы:

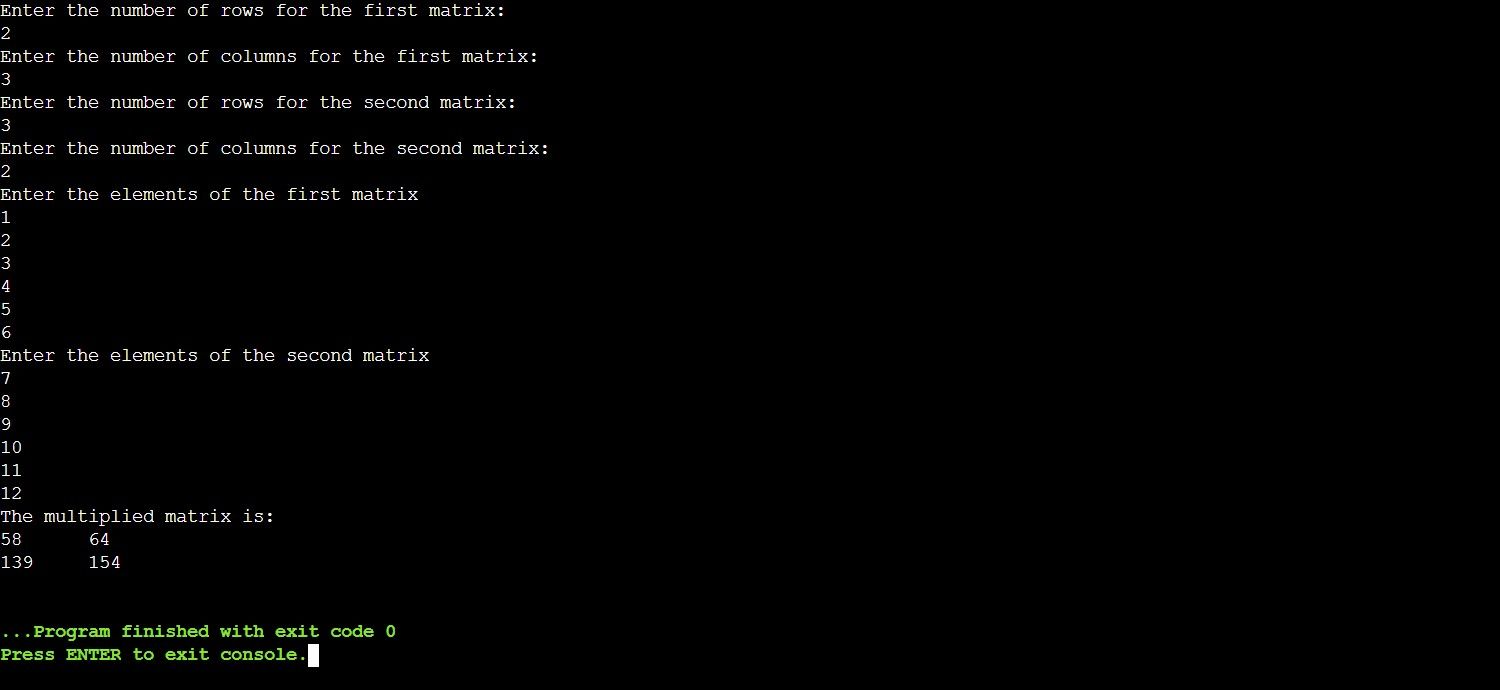
Если ввод несовместим, отобразится сообщение об ошибке:

Важно: в примере используется VLA (variable length arrays). VLA поддерживаются в стандарте C99 и позже, но не поддерживаются всеми компиляторами (например, MSVC это не поддерживает). Для переносимости можно использовать динамическое выделение через malloc.

Сложность и ресурсы (факт‑бокс)

• Временная сложность наивного алгоритма: O(r1 c2 c1). Для квадратных n×n матриц это O(n^3).
• Память для результата: O(r1 * c2).
• Альтернативы по скорости: алгоритм Штрассена ~O(n^2.807), алгоритмы Улума и дальнейшие — ещё быстрее, но сложнее в реализации.

Факт: на практике для численных задач чаще используют оптимизированные библиотеки (BLAS, LAPACK), которые учитывают кэш, векторизацию и многопоточность.

Когда умножение матриц невозможно — типичные ошибки

• Неправильно введены размеры: часто путают строки и столбцы при вводе.
• Использование неподходящих типов: переполнение int при больших значениях. Для больших чисел используйте long long или плавающую точку.
• Некорректная инициализация результата: если не обнулять mul[i][j], накопление выдаст ложный результат.
• Неучтённая совместимость компилятора: VLA в C не универсальны.

Альтернативные подходы и оптимизации

1. Библиотеки и высокоуровневые инструменты
   • В научных и прикладных системах используйте BLAS (OpenBLAS, Intel MKL) и LAPACK.
   • В Python используйте numpy.dot или @, они вызывают оптимизированные библиотеки.
2. Алгоритмические улучшения
   • Алгоритм Штрассена уменьшает число операций умножения, полезен для очень больших матриц.
   • Алгоритмы, использующие блокирование (blocking/tile), улучшают работу с кэшем.
3. Параллельность
   • Многопоточность (OpenMP) и вычисления на GPU (CUDA, OpenCL) дают большие выигрыши для больших матриц.
4. Типы данных
   • Для целых значений выбирайте достаточный битовый размер, чтобы избежать переполнения.
   • Для научных расчётов часто используют double для точности.

Руководство по оптимизации (мини‑методология)

1. Начните с корректной, но простой реализации.
2. Измерьте производительность с тестами реального размера.
3. Примените блокирование, чтобы улучшить локальность данных.
4. Профилируйте: найдите узкие места (cache misses, память, загрузка CPU).
5. Если нужно — используйте библиотеку BLAS или перенос на GPU.
6. Повторно замерьте и верифицируйте точность результатов.

Пример блокирования (идея)

Идея: делить матрицы на небольшие блоки размером b×b и выполнять умножение блоков. Это уменьшает количество промахов кэша и часто даёт большую реальную скорость при малых изменениях алгоритма.

Decision flow — проверка возможности умножения (Mermaid)

flowchart TD
  A[Ввод размеров A и B] --> B{c1 == r2?}
  B -- Да --> C[Разрешено: продолжить ввод элементов]
  B -- Нет --> D[Ошибка: несоответствие размеров]
  C --> E[Инициализация mul нулями]
  E --> F[Выполнить тройной цикл i,j,k]
  F --> G[Вывести результат]

Тесты, контрольные случаи и критерии приёмки

Контрольные случаи:

• Малые размерности: 1×1 с 1×1.
• Несовместимые размеры: 2×3 и 4×2 (ошибка).
• Матрицы с нулями и единицами: проверка идёмности для единичной матрицы.
• Большие значения: тест на переполнение (использовать 64‑бит).

Критерии приёмки:

• Корректность результата для контрольных матриц.
• Обработка ошибок (неправильные размеры) с понятным сообщением.
• Понятный формат ввода/вывода.
• Отсутствие утечек памяти (если используется malloc).

Роль‑ориентированные чеклисты

• Студент:
  • Понимание условий совместимости.
  • Умение выполнить ручный пример 2×3 × 3×2.
• Разработчик приложения:
  • Тесты на граничные случаи.
  • Обработка ошибок ввода.
• Data scientist / инженер ML:
  • Использовать оптимизированные библиотеки (numpy, BLAS).
  • Проверить числовую стабильность и представление данных.
• HPC‑инженер:
  • Параллельная реализация, блокирование, GPU.

Совместимость и советы для C‑реализаций

• VLA (int a[r][c]) поддерживается в C99 и частично в C11, но MSVC его не поддерживает. Для переносимости используйте malloc и массив указателей или одномерный массив размером r*c.
• Для больших матриц массивы на стеке могут переполнить стек. Выделяйте память динамически.
• При целочисленных операциях контролируйте переполнение и используйте более широкие типы при необходимости.

Пример выделения через malloc (идея):

int *m1 = malloc(r1 * c1 * sizeof(int));
// элемент (i,j) хранится как m1[i*c1 + j]

Контрпримеры и случаи, когда наивный алгоритм не подходит

• Очень большие матрицы (миллионы элементов): наивная реализация медленна и требует много памяти.
• Когда требуется высокая производительность — используйте BLAS или GPU.
• Для разреженных матриц (sparse) использовать наивный dense алгоритм — неэффективно; применяйте sparse‑форматы и специальные алгоритмы.

Короткий словарь терминов

• Матрица — двумерный массив чисел.
• Вектор — одномерный массив (строка или столбец).
• Скалярное произведение — сумма попарных произведений.
• VLA — переменная длина массива в C.

Шаблон тест‑кейса (пример)

• Описание: умножение A(2×3) на B(3×2).
• Вход: A=[[1,2,3],[4,5,6]]; B=[[7,8],[9,10],[11,12]].
• Ожидаемый выход: [[58,64],[139,154]].
• Критерии: совпадение всех элементов; корректный формат вывода.

Краткое резюме

Умножение матриц — базовая, но важная операция во многих задачах. Главное правило — число столбцов первой матрицы должно совпадать с числом строк второй. Наивный тройной цикл прост в реализации и наглядно показывает суть операции, но при масштабировании имеет ограничения по производительности. Для реальных задач используйте оптимизированные библиотеки, технику блокирования и параллелизацию.

Понравилось руководство? Начните с небольшой реализации, проверьте её тестами из раздела, затем попробуйте оптимизировать или подключить библиотеку BLAS для реальных данных.