Калибровочная кривая в Excel: как построить, проверить и применять

Простая калибровочная кривая — это прямая, построенная по известным эталонным парам значений (X — стандарты, Y — показания прибора). В Excel это удобно делать через диаграмму «Точечная (XY)», добавить трендлайн и вывести формулу и R². Для автоматических расчётов используйте функции SLOPE, INTERCEPT и CORREL, а затем подставьте их в выражения для вычисления неизвестных X или Y.

В этой статье: понятие калибровочной кривой, пошаговая инструкция в Excel, как получить коэффициенты линии и R², как настроить формулы для быстрого расчёта, проверочные критерии, типичные ошибки и практическая шпаргалка.

Быстрые ссылки

• Что такое калибровочная кривая и зачем использовать Excel
• Пример и пошаговая инструкция
• Как вычислить SLOPE, INTERCEPT и R²
• Как подготовить формулы для быстрого расчёта
• Когда метод не применим и альтернативы

Что такое калибровочная кривая и как Excel помогает при её создании

Калибровочная кривая — это математическое соответствие между известными значениями стандарта (X) и ответом прибора (Y). Типичный пример — калибровка термометра: два эталона (точки замерзания и кипения воды) дают две пары (X, Y), по которым можно провести линию и затем по показанию прибора определить истинную температуру.

Определение в одну строку: калибровочная кривая — это модель (чаще линейная), позволяющая переводить показания прибора в истинные значения.

Почему Excel удобен:

• Встроенные диаграммы для быстрой визуализации пар (X, Y).
• Добавление трендлайна с показом уравнения прямо на графике.
• Функции статистики (SLOPE, INTERCEPT, CORREL) для точных вычислений без ручного вывода коэффициентов.
• Простая подстановка коэффициентов в формулы для массовых расчётов.

Важно: линейная кривая подходит только если связь между X и Y примерно линейна. При существенной нелинейности следует использовать полиномиальные трендлайны или специальные методы регрессии.

Пример: набор данных и общая идея

В примере ниже мы используем серию из десяти пар данных (X — стандарты, Y — ответы прибора). X может быть концентрацией раствора; Y — показанием прибора. После построения диаграммы мы добавим трендлайн, посмотрим формулу Y = Mx + B и R², а затем рассчитаем коэффициенты SLOPE и INTERCEPT средствами Excel, чтобы использовать их в формулах для быстрого вычисления неизвестных.

Подготовка данных

В простейшем случае таблица содержит две колонки: X-Value и Y-Value. Введите значения в соседние столбцы — Excel распознает диапазоны при построении диаграммы.

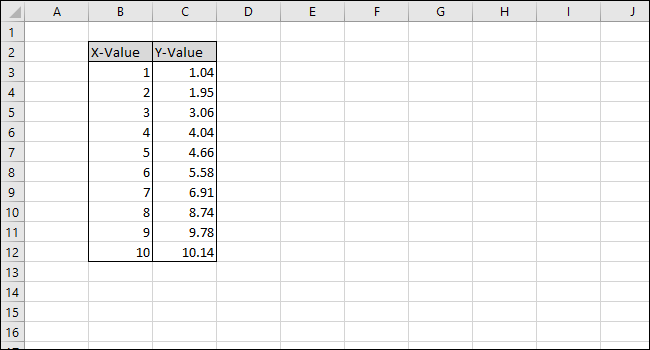
Совет: используйте заголовки столбцов и форматируйте диапазон как таблицу Excel (Ctrl+T) — так удобнее ссылаться на колонки по именам.

Шаг 1: создать диаграмму (точечная диаграмма XY)

Подробные шаги с пояснениями и поясняющими снимками:

1. Выделите столбец с X-значениями.

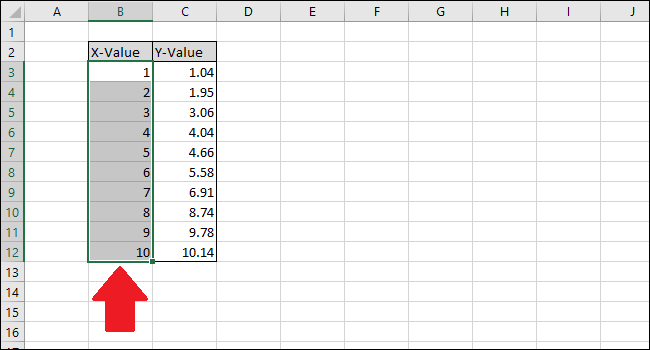
2. Удерживая Ctrl, выделите столбец с Y-значениями.

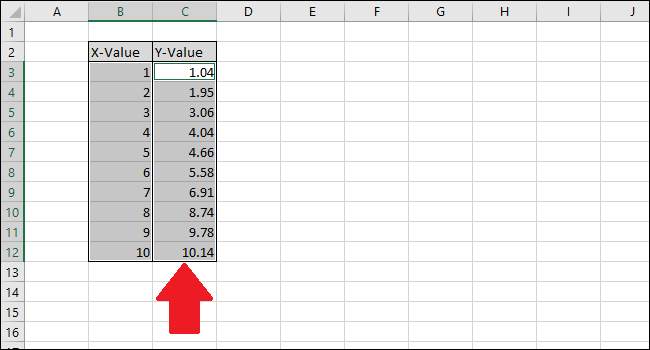
3. Перейдите на вкладку “Вставка”.

4. В группе диаграмм выберите тип “Точечная (XY)” и первый вариант (только точки).

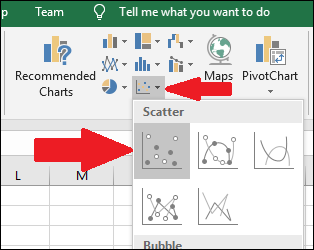
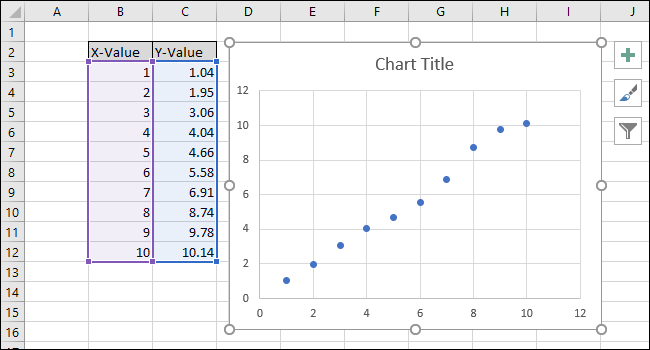
5. Excel отобразит диаграмму с точками данных.

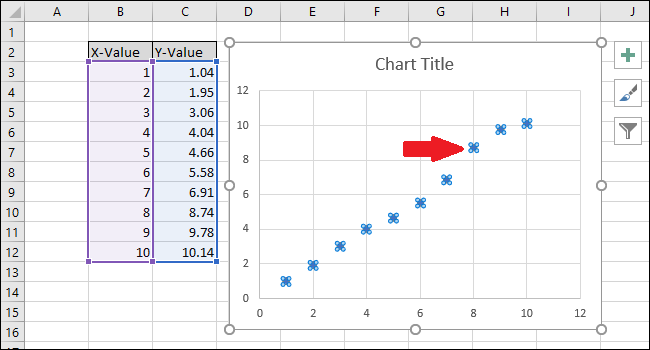
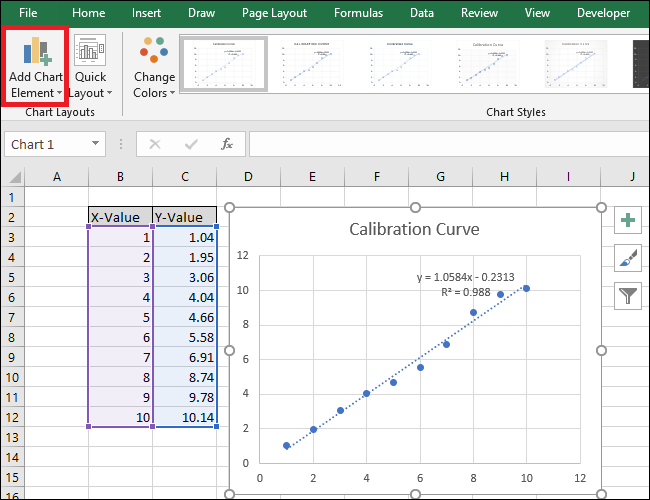
6. Щёлкните по одной из точек, чтобы выделить серию данных. Точки будут обведены.

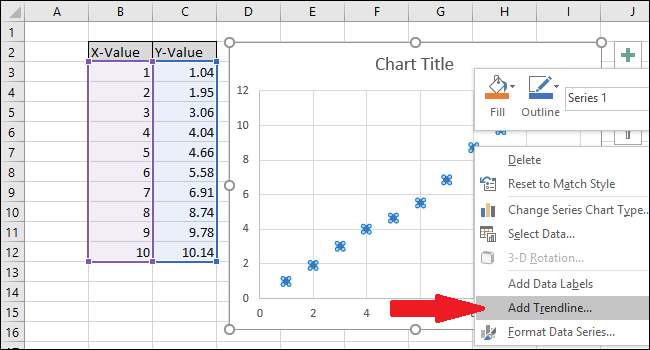
7. Правый клик по серии → Добавить линию тренда.

8. На диаграмме появится прямая.

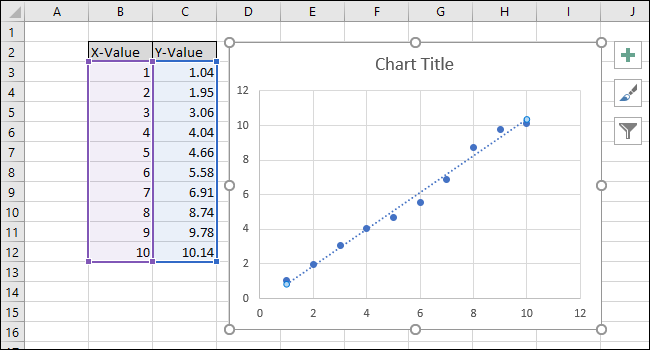
9. В панели форматирования линии тренда установите флажки “Отобразить уравнение на диаграмме” и “Отобразить значение R-квадрат на диаграмме”.

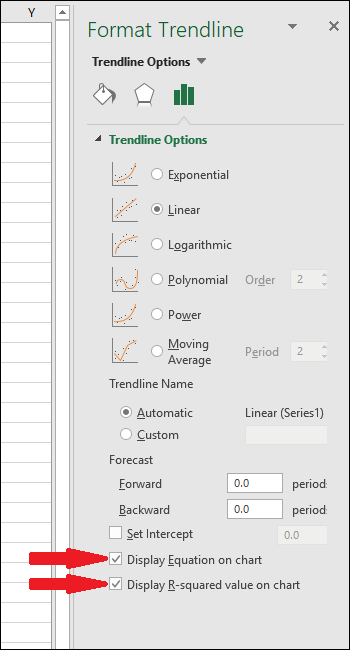
10. Уравнение (Y = Mx + B) и R² появятся на графике.

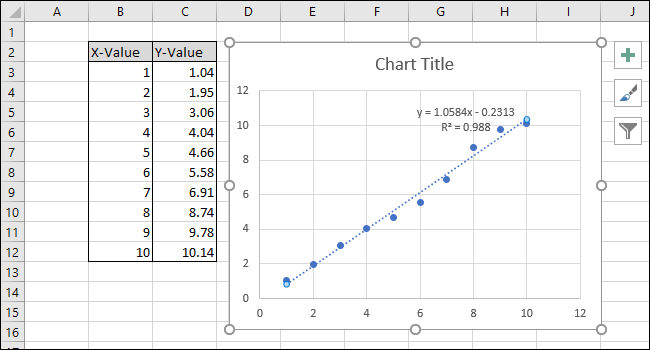
Пояснение R²: это мера соответствия модели данным. R² = 1 означает идеальную подгонку; R² близкое к 0 — модель плохо объясняет вариацию. Для практических измерений обычно стремятся к максимально возможному R² в рамках методов и ограничения приборов.

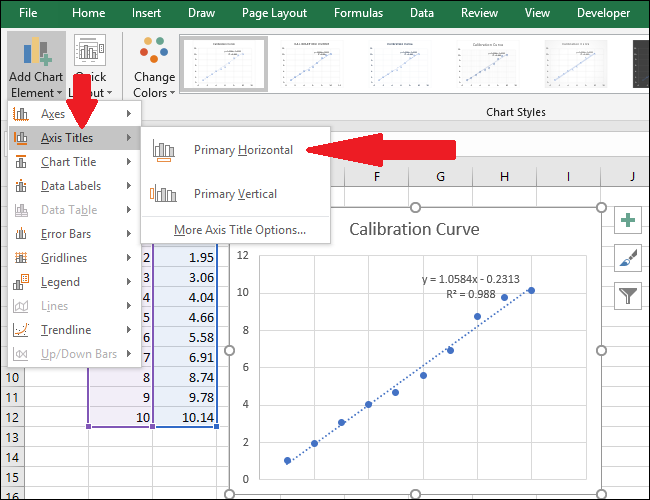
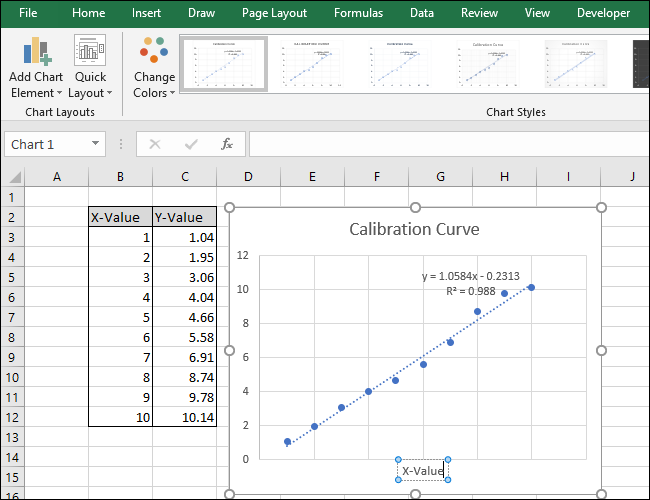
11. Подпишите заголовок графика и оси:

• Клик по заголовку → введите понятное название.

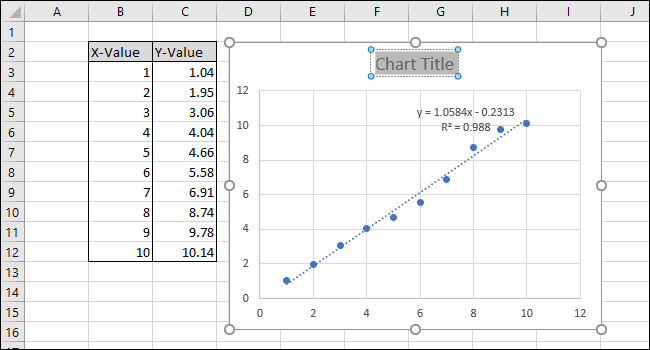
• Через Инструменты диаграмм → Конструктор → Добавить элемент диаграммы → Заголовки осей → Основная горизонтальная/вертикальная. Затем переименуйте подписи.

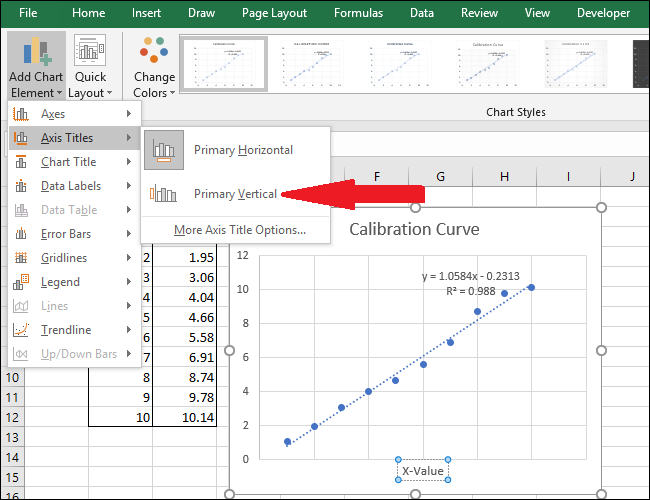
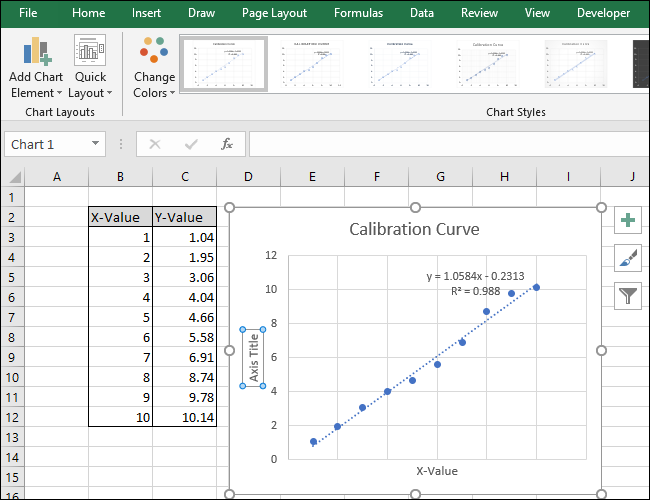
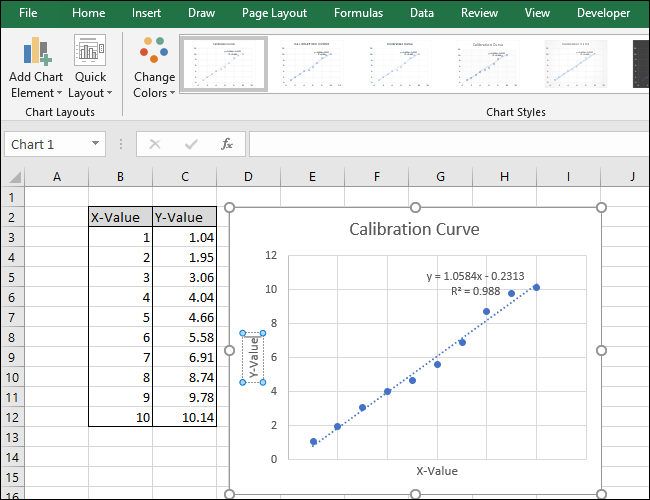
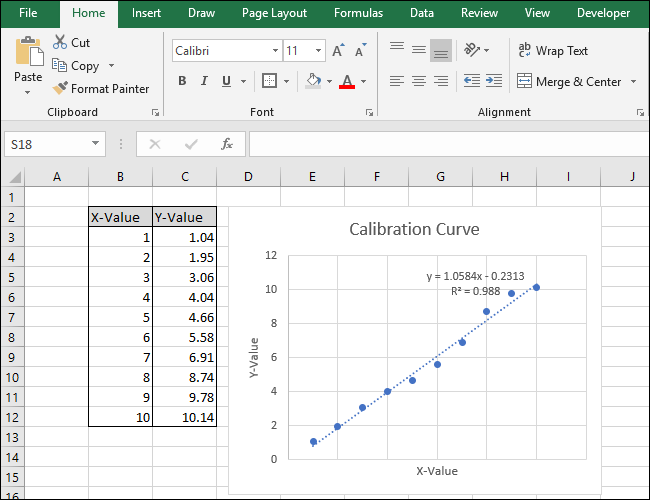
Советы по визуализации:

• Укажите единицы измерения в подписях осей (например, «Концентрация, мг/л» или «Температура, °C»).
• При большом разбросе данных включите сетку и маркеры.
• При наличии выбросов проверьте измерения и при необходимости повторите эксперимент.

Шаг 2: вычисление коэффициентов и R² функциями Excel

Ниже показано, как получить те же значения, что и уравнение трендлайна, но численно в ячейках с помощью функций.

1. Введите заголовки для вычислений (например, SLOPE, INTERCEPT, R-squared) в строке под таблицей данных.

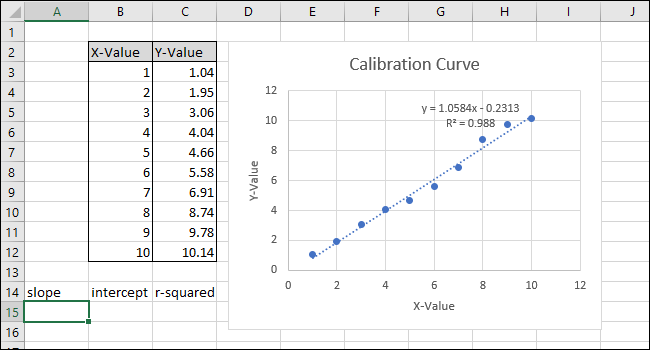
2. Вычисление SLOPE:

• Формулы → Дополнительные функции → Статистические → SLOPE.

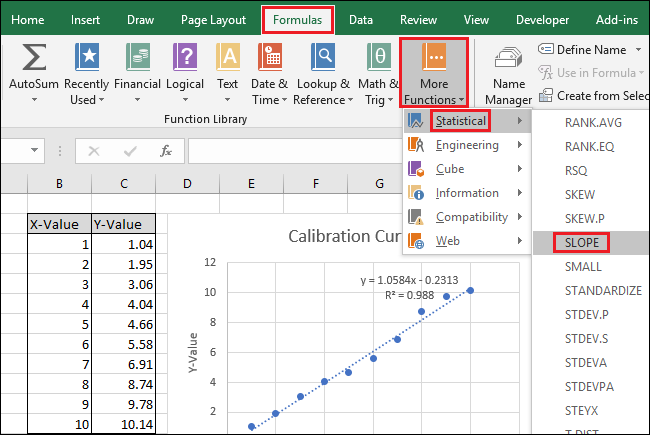
• В поле Known_ys укажите диапазон Y (ответы прибора).

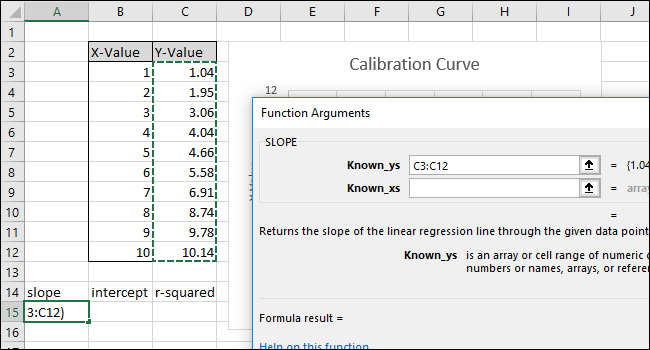
• В поле Known_xs укажите диапазон X (эталоны). Порядок аргументов важен.

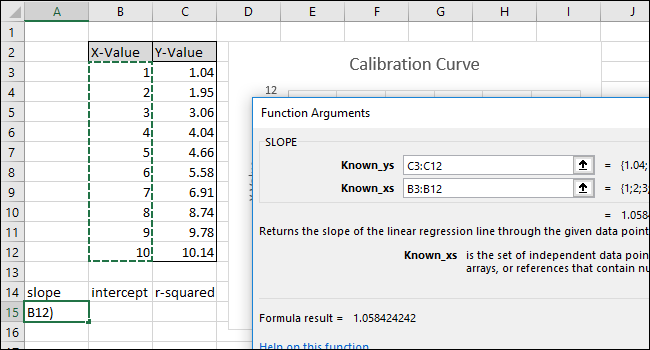
• Формула в строке формул будет выглядеть как

=SLOPE(C3:C12,B3:B12)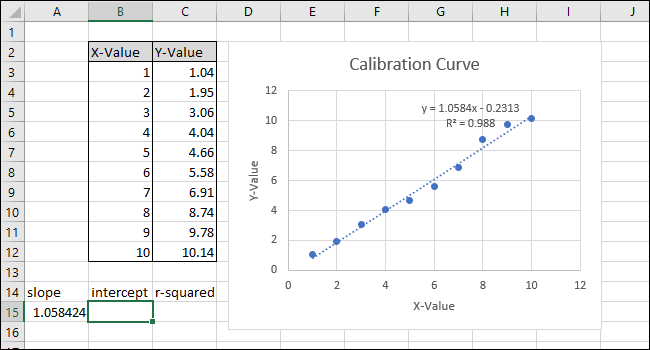

3. Вычисление INTERCEPT:

• Формулы → Дополнительные функции → Статистические → INTERCEPT.

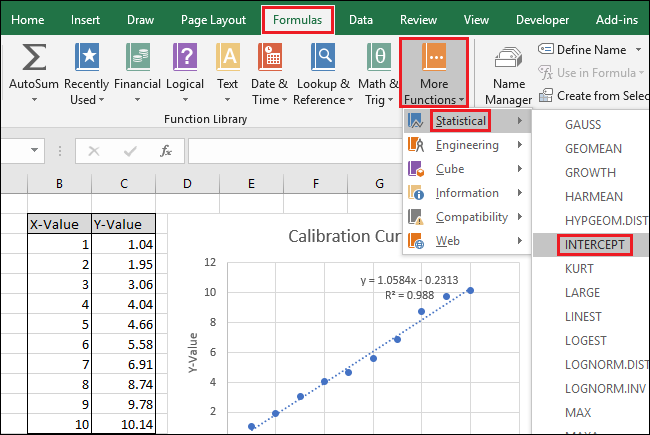
• Аналогично, укажите Known_ys (Y) и Known_xs (X).

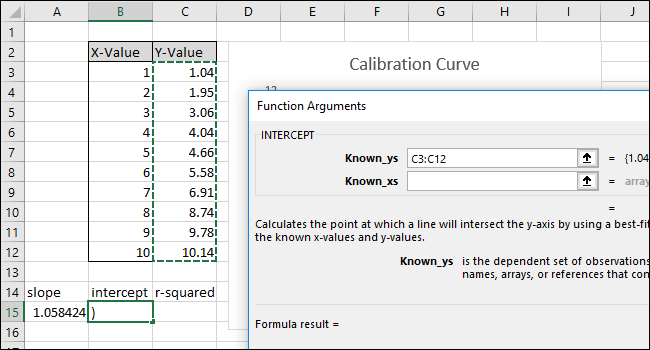
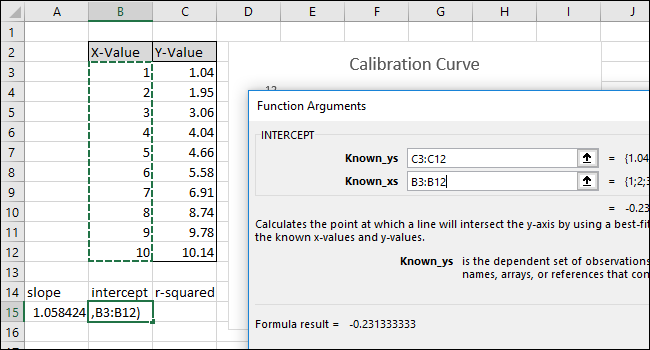
• Формула будет выглядеть как

=INTERCEPT(C3:C12,B3:B12)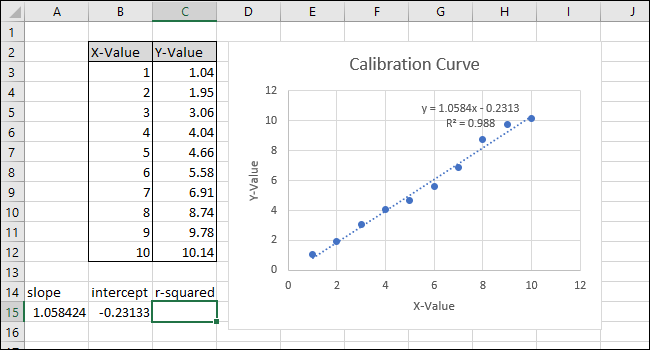

4. Вычисление R-квадрат через CORREL:

• Формулы → Дополнительные функции → Статистические → CORREL.

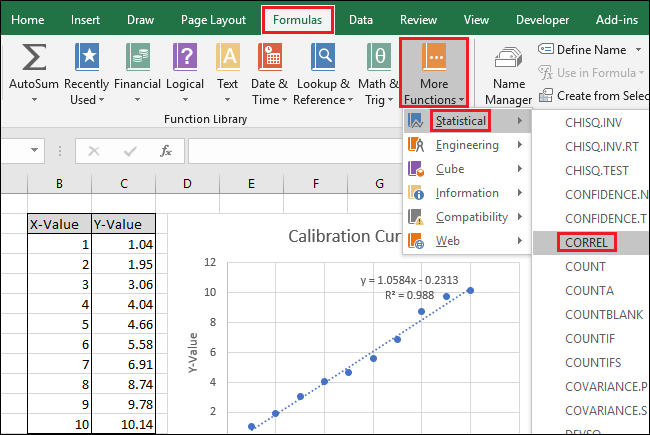
• CORREL возвращает коэффициент корреляции R (не R²). Чтобы получить R², возведите результат в квадрат.

=CORREL(B3:B12,C3:C12)^2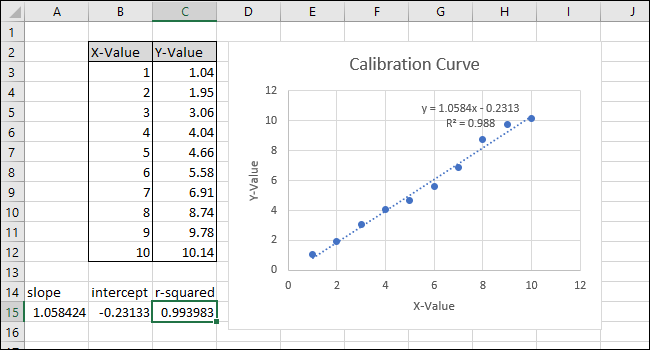

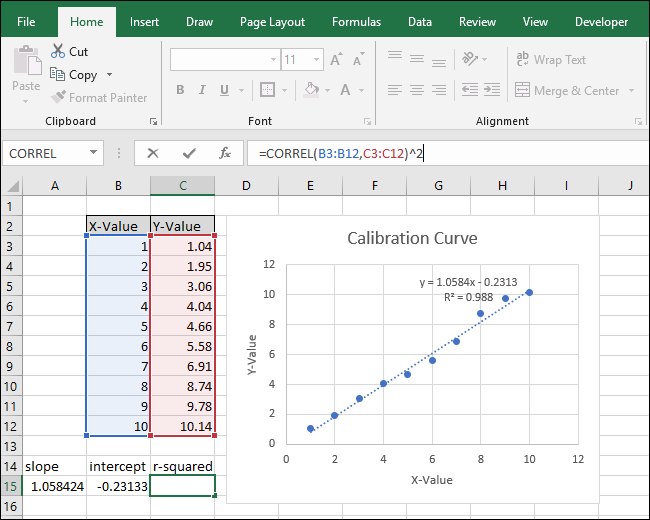
После этого численные значения SLOPE и INTERCEPT в ячейках должны совпадать с M и B в уравнении, которое отображается на диаграмме.

Шаг 3: формулы для быстрого вычисления неизвестных X или Y

Теперь можно подставлять значения, чтобы быстро получать искомые величины.

Уравнение прямой:

Y = SLOPE * X + INTERCEPT

• Чтобы получить Y по заданному X, используйте простую формулу:

= $SLOPE$ * X_input + $INTERCEPT$

• Чтобы вычислить X по заданному Y, выражение переставляется:

= (Y_input - $INTERCEPT$) / $SLOPE$

Где $SLOPE$ и $INTERCEPT$ — абсолютные ссылки на ячейки с вычисленными коэффициентами, чтобы формулы можно было копировать.

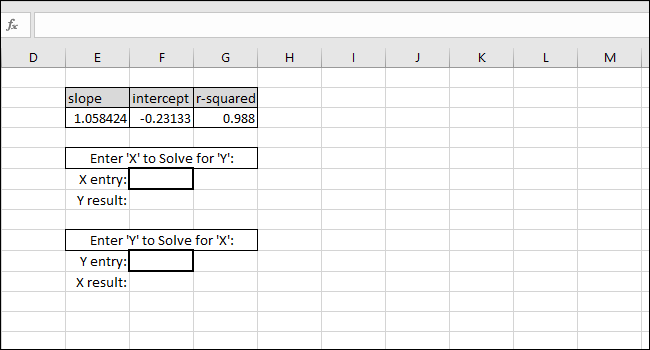
Примеры и пояснения из демонстрации:

• Если X_input = 0, то Y = INTERCEPT. Это можно использовать для быстрой проверки корректности формул.

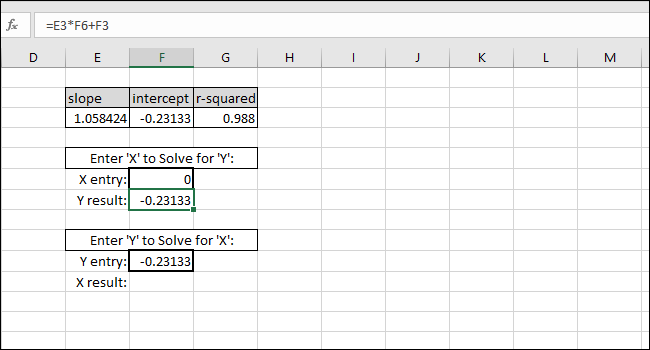
• Если при подстановке Y = INTERCEPT вы ожидаете X = 0, но получаете значение порядка 1e-6, проверьте точность и формат ячеек: часто причина — усечение/округление вводимого числа.

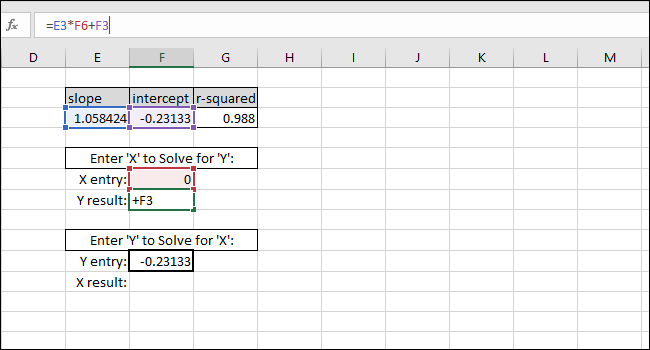
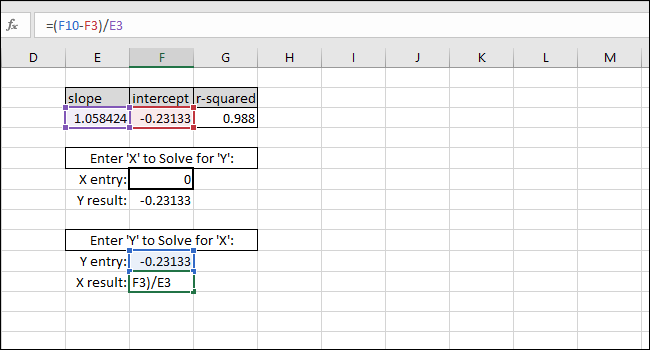
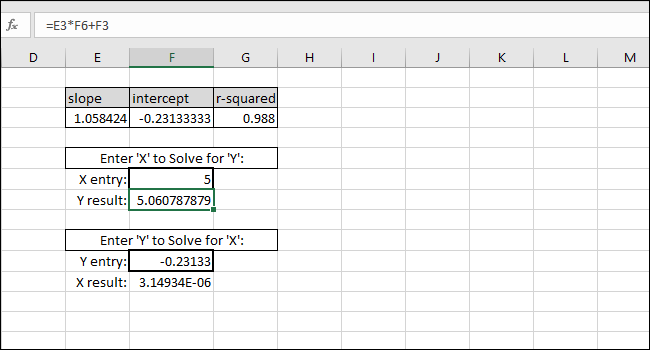
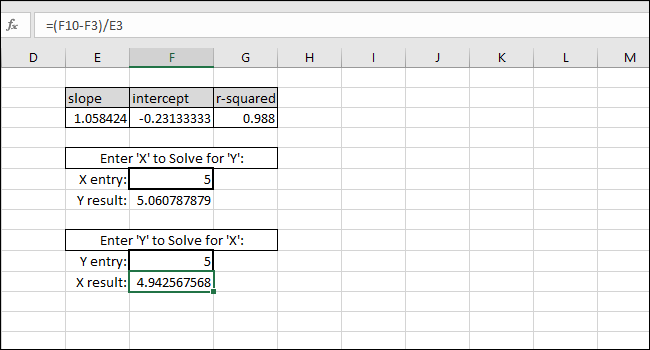
Практический результат: при показании прибора 5 единиц калибровка в примере даёт оценку истинного значения 4.94.

Проверка корректности: критерии приёмки

• Совпадение M и B на графике и в ячейках SLOPE/INTERCEPT.
• R² близко к ожидаемой величине для вашей методики (для линейных задач — чем выше, тем лучше). Не существует универсального порога, но R² ниже 0.7 обычно сигнализирует о слабой линейности.
• Отсутствие систематических отклонений: остатки (расстояния точек до линии) не должны зависеть от X.
• При многократных измерениях повторяемость результатов в пределах допустимой погрешности.

Критерии приёмки нужно заранее прописать для каждого процесса калибровки: допустимые пределы остатка, требования к R², правила работы с выбросами.

Шпаргалка формул (чек‑лист)

• Получить наклон (slope):

=SLOPE( known_ys , known_xs )

• Получить пересечение с осью Y (intercept):

=INTERCEPT( known_ys , known_xs )

• Получить R (коэффициент корреляции):

=CORREL( range1 , range2 )

• R-квадрат:

=CORREL(range1, range2)^2

• Вычислить Y по X:

= SLOPE_cell * X_input + INTERCEPT_cell

• Вычислить X по Y:

= ( Y_input - INTERCEPT_cell ) / SLOPE_cell

Совет: используйте абсолютные ссылки ($A$1) на ячейки со SLOPE и INTERCEPT.

Когда линейная калибровка не работает: примеры и альтернативы

Контрпримеры/когда метод не подходит:

• Нелинейная зависимость (экспоненциальная, логарифмическая): прямая даёт плохую подгонку, низкий R² и систематические остатки.
• Ограниченный диапазон: если прибор нечувствителен в части диапазона, линейная модель неточна.
• Наличие сильных выбросов или ошибок измерений.

Альтернативные подходы:

• Полиномиальная регрессия (трендлайн степени 2 или 3 в Excel) — когда зависимость криволинейна.
• Логарифмическая/экспоненциальная аппроксимация — для специфических физических процессов.
• Нелинейная регрессия в специализированных инструментах (R, Python/scipy/statsmodels) для точной аппроксимации.
• Калибровка методом наименьших квадратов с учётом ошибок и взвешенной регрессии при неодинаковой дисперсии измерений.

Риски и смягчение

• Риск: неверная интерпретация R² как гарантии правильности. Смягчение: анализ остатков и проверочные измерения.
• Риск: округление коэффициентов вручную. Смягчение: используйте ячейки с точными значениями SLOPE/INTERCEPT, а не копируйте текст из графика.
• Риск: отрицательный или нулевой SLOPE, когда физический смысл противоречит этому. Смягчение: проверить данные, повторить измерения.

Мини‑методология (шаги для воспроизведения)

1. Подготовить не менее 5—10 эталонных пар (X, Y) по возможности равномерно по диапазону.
2. Ввести данные в таблицу, оформить как таблицу Excel.
3. Построить точечную диаграмму (XY), добавить трендлайн — проверить визуально.
4. Вычислить SLOPE, INTERCEPT и CORREL^2 в отдельных ячейках.
5. Проанализировать остатки и R². При необходимости сменить модель.
6. Ввести формулы для автоматических вычислений X или Y.
7. Зафиксировать протокол калибровки и сохранить файл с датами и ответственными.

Роль‑ориентированные чек‑листы

Лаборант/техник:

• Собрать и записать эталонные значения X и измеренные Y.
• Проверить целостность оборудования и калибровку стандартов.
• Выполнить расчёт и сохранить файл в репозитории.

Аналитик/инженер данных:

• Проверить корректность регрессионной модели (остатки, R²).
• Оценить необходимость перехода на нелинейную модель.
• Автоматизировать расчёты и добавить проверки ошибок ввода.

Разработчик/интегратор:

• Внедрить коэффициенты SLOPE и INTERCEPT в код устройства/ПО с контролем версий.
• Обеспечить обработку граничных случаев и логирование.

Краткий глоссарий в одну строку

• Эталон (standard): известное истинное значение X.
• Ответ прибора (response): измеренное значение Y.
• SLOPE: наклон прямой, изменение Y на единицу X.
• INTERCEPT: значение Y при X=0.
• R²: доля вариации Y, объяснённая моделью.

Типичные ошибки и как их избегать

• Копирование формулы из диаграммы (текст) и округление коэффициентов — избегайте, используйте функции SLOPE/INTERCEPT.
• Игнорирование выбросов — проверьте измерения и источники ошибок.
• Применение линейной модели там, где связь явно нелинейна — сначала визуализируйте остатки.

Пример рабочего регламента для записи калибровки

• Название процедуры: ежемесячная калибровка аналитического прибора.
• Входные данные: список эталонов (X) и серия измерений (Y).
• Выходные данные: файл Excel с диаграммой, вычисленными SLOPE/INTERCEPT, R², подпись ответственного.
• Критерий успешности: R² ≥ требуемого порога и остатки в допустимых пределах.

Заключение

Калибровочная кривая в Excel — простой и доступный способ перевода показаний прибора в истинные значения при линейной зависимости. Главное — верно построить диаграмму, вычислить коэффициенты SLOPE и INTERCEPT, проверить качество модели через R² и анализ остатков, а затем внедрить проверенные формулы для повседневных расчётов.

Важно выполнять валидацию модели и иметь регламент, описывающий критерии приёмки и действия при низком качестве подгонки.

В следующих действиях можно расширить процедуру: автоматизировать загрузку данных, добавить отчётность с контрольными картами и хранить историю калибровки с отметками об ответственном лице и дате.

Источник иллюстраций: пошаговые снимки экрана Excel с демонстрацией построения диаграммы и использования функций.

Важное: всегда сохраняйте и версионируйте файл калибровки и записывайте дату/ответственного за изменение коэффициентов.