Testes estatísticos em Python: como validar seus dados

Atualização

• Uma versão anterior deste artigo confundiu as definições de falsos positivos e falsos negativos. Um erro do Tipo I é um falso positivo, e um erro do Tipo II é um falso negativo. HTG lamenta o erro.

Links rápidos

• O que é teste de hipótese
• Por que testes estatísticos
• t-test de Student
• Regressão linear
• ANOVA
• Testes não paramétricos

O que é teste de hipótese?

Teste de hipótese é o conjunto de técnicas estatísticas usadas para verificar se um resultado observado em uma amostra é compatível com o acaso ou indica um efeito real. Em uma única linha: o teste confronta uma hipótese nula (H0), que assume ausência de efeito, com uma hipótese alternativa (H1), que propõe que existe um efeito.

Definir H0 e H1 antes de olhar para os dados é uma regra prática importante para evitar viés de confirmação. A analogia jurídica ajuda: H0 é a presunção de inocência — você só a rejeita se houver evidências suficientes.

Exemplo prático: um ensaio clínico onde um grupo recebe placebo e outro a droga. Se queremos saber se a droga reduz a pressão arterial sistólica, comparamos a média entre os grupos e aplicamos um teste estatístico apropriado.

Importante: em testes frequencistas você trabalha com níveis de significância (alpha) e p-values. Alpha = 0,05 corresponde a 95% de confiança; alpha = 0,01 corresponde a 99% de confiança. Rejeitamos H0 quando p < alpha.

Atualização: 27/09/2025 10:54 EST por David Delony

Em testes de hipótese podem ocorrer dois erros principais:

• Erro do Tipo I (falso positivo): rejeitar H0 quando H0 é verdadeira. Consequência: dizer que há efeito quando não há.
• Erro do Tipo II (falso negativo): não rejeitar H0 quando H1 é verdadeira. Consequência: perder um efeito real.

A melhor defesa contra ambos é aumentar o tamanho da amostra e planejar o estudo (power analysis) antes de coletar dados.

Por que usar testes estatísticos?

Porque a simples observação de diferenças não prova causalidade ou significância. Um gráfico pode sugerir uma diferença, mas testes estatísticos quantificam a probabilidade de que essa diferença tenha surgido por acaso.

Testes são parte técnica, parte pensamento crítico: escolha do teste, verificação de pressupostos, controle de comparações múltiplas e interpretação de efeito (size) são tão importantes quanto o p-value.

t-test de Student

O t-test foi desenvolvido para situações em que a distribuição se aproxima da normal e a variância populacional é desconhecida. Ele compara médias: seja a média de uma amostra contra um valor hipotético (one-sample), duas amostras independentes (independent) ou duas amostras pareadas (paired).

Termo rápido: p-value é a probabilidade, sob H0, de obter um resultado tão extremo quanto ou mais extremo que o observado. Não é a probabilidade de H0 ser verdadeira.

Exemplo com Python e Pingouin. Primeiro, importamos NumPy e o gerador de números aleatórios:

import numpy as np
rng = np.random.default_rng()

Geramos uma amostra com 15 valores da normal padrão:

a = rng.standard_normal(15)

Antes de aplicar o t-test, verifique o pressuposto de normalidade em amostras pequenas usando o teste de Shapiro-Wilk (Pingouin):

import pingouin as pg
pg.normality(a)

Agora testamos a hipótese nula de que a média é 0,45:

pg.ttest(a, .45)

Se o p-value for 0,99 não rejeitamos H0 com alpha = 0,05 nem com alpha = 0,01. Ou seja: a amostra não fornece evidência de que a média difira de 0,45.

Boas práticas com t-test:

• Verifique normalidade (Shapiro-Wilk para amostras pequenas).
• Verifique homogeneidade de variâncias quando comparar duas amostras (Levene ou similar).
• Use o teste pareado quando os dados forem dependentes (mesmos indivíduos medidos antes/depois).
• Reporte intervalo de confiança e tamanho do efeito (por exemplo, Cohen’s d).

Regressão linear

Regressão linear ajusta uma reta y = a + b*x para explicar a relação entre variáveis. O teste estatístico típico aqui testa se o coeficiente angular (b) é igual a zero (H0: b = 0). Um p-value pequeno indica que é improvável que a inclinação seja zero.

Usamos Seaborn para visualização e Pingouin para análise formal. Exemplo com dataset de gorjetas (tips) do Seaborn:

import seaborn as sns
tips = sns.load_dataset('tips')

Inspecione os primeiros registros com pandas:

tips.head()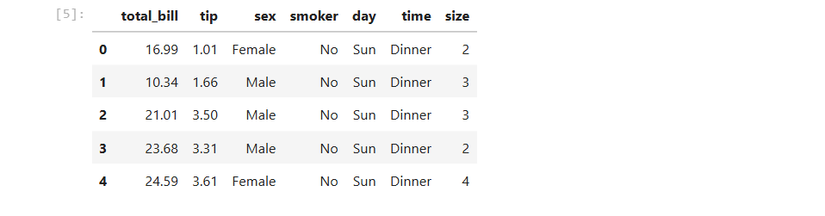

Plote uma regressão entre total_bill (x) e tip (y):

sns.regplot(x='total_bill', y='tip', data=tips)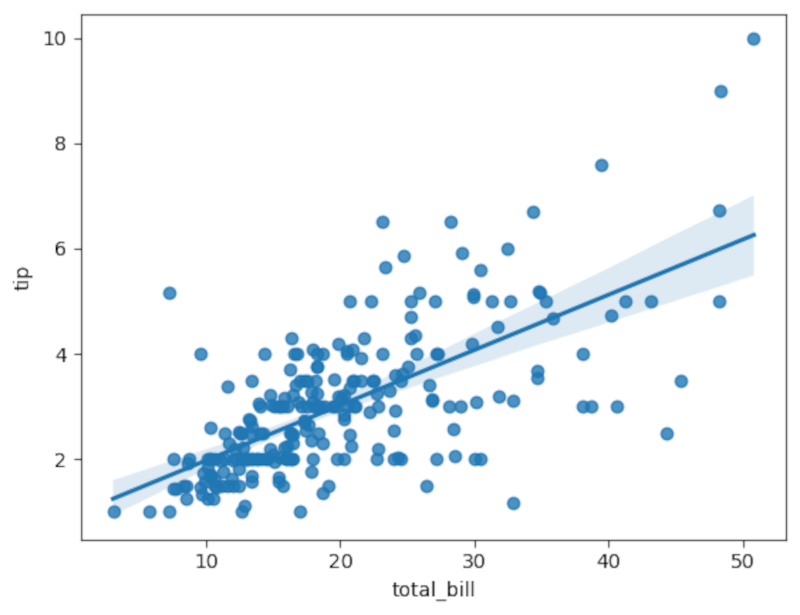

Para análise formal com Pingouin:

pg.linear_regression(tips['total_bill'], tips['tip']).round(2)

A tabela resultante inclui coeficientes, t-value e p-value. Um t-value alto e p-value próximo de zero permitem rejeitar H0: b = 0. Sempre verifique também R² (explicação da variância) e resíduos (para checar heterocedasticidade e normalidade dos resíduos).

ANOVA

ANOVA (Analysis of Variance) testa diferenças entre médias de três ou mais grupos. A hipótese nula é que todas as médias dos grupos são iguais. ANOVA compara variabilidade entre grupos com variabilidade dentro de grupos.

Exemplo: tamanho das nadadeiras (flipper_length_mm) por espécie em um dataset de pinguins:

penguins = pg.read_dataset('penguins')
pg.anova(data=penguins, dv='flipper_length_mm', between='species').round(2)

Se p-value for 0,0 (ou muito pequeno) rejeitamos H0: conclui-se que espécie é um preditor significativo de comprimento de nadadeira. Após ANOVA, use testes post-hoc (Tukey, pairwise t-tests com correção) para saber quais grupos diferem entre si.

Testes não paramétricos

Muitos testes paramétricos assumem uma distribuição (normalidade). Dados do mundo real podem ser assimétricos ou conter outliers; aí entramos nos testes não paramétricos, que não supõem uma distribuição específica.

Mann-Whitney U (MWU) é análogo não paramétrico ao t-test para duas amostras independentes:

a = rng.random(15)
b = rng.random(15)
pg.mwu(a, b)

Kruskal-Wallis é a versão não paramétrica de ANOVA:

pg.kruskal(data=penguins, dv='flipper_length_mm', between='species').round(2)

Os resultados podem ser similares aos paramétricos quando os pressupostos são satisfeitos, mas mais robustos quando há violação de pressupostos.

Interpretação correta dos resultados

• p-value baixo não implica grande efeito prático. Sempre reporte tamanho do efeito (effect size) e intervalos de confiança.
• Significância estatística não é o mesmo que significância clínica ou comercial.
• Em amostras grandes, efeitos pequenos podem ser estatisticamente significativos.
• Em amostras pequenas, poder baixo aumenta chance de erro Tipo II.

Importante: ajustar para múltiplas comparações. Se você testa 20 hipóteses, espere aproximadamente 1 significativo a 5% por acaso. Use Bonferroni, Holm ou FDR onde fizer sentido.

Quando os testes falham ou enganam

• Dados não independentes: usar testes que assumem independência (ex.: amostras pareadas vs independentes) pode invalidar resultados.
• Violação de pressupostos sem correção: por exemplo, heterocedasticidade não tratada pode falsificar p-values.
• Amostragem enviesada: não é problema do teste; é problema do desenho do estudo.
• P-hacking e exploração excessiva: escolher testes ou subconjuntos com base em onde os p-values são baixos leva a resultados não replicáveis.

Contraexemplos rápidos:

• Gráficos com grandes diferenças visuais que não são significativas quando a variação interna é enorme.
• Pequenas diferenças em grandes amostras que são estatisticamente significativas, mas irrelevantes na prática.

Alternativas e complementos aos testes clássicos

• Métodos bayesianos (Bayes Factors, intervalos credíveis) oferecem uma interpretação direta da probabilidade de parâmetros.
• Bootstrap e reamostragem: estimativas de intervalo sem presumir normalidade.
• Modelos mistos (mixed-effects) para dados hierárquicos (medidas repetidas, clusters).
• Machine learning com validação cruzada para predição em vez de inferência.

Mini-metodologia: como conduzir um teste em Python passo a passo

1. Defina pergunta e hipóteses (H0 e H1).
2. Planeje tamanho amostral (power analysis) e nível de alpha.
3. Coleta de dados com critérios claros.
4. Exploração inicial: gráficos, estatísticas descritivas, outliers.
5. Verificação de pressupostos (normalidade, homogeneidade, independência).
6. Escolha do teste apropriado (paramétrico vs não paramétrico; pareado vs independente).
7. Execução do teste e inspeção de p-value, t-value ou estatística relevante.
8. Reporte: p-value, tamanho do efeito, intervalo de confiança, checagem de pressupostos.
9. Se necessário, correções para múltiplas comparações e análise post-hoc.

Checklist por função

Data scientist

• Definiu H0/H1 e alpha antes da análise
• Fez power analysis
• Testou pressupostos
• Reportou tamanhos de efeito e ICs
• Aplicou correções para múltiplas comparações

Analista de negócio

• Validou que diferença estatística reflete impacto de negócio
• Exigiu métricas de efeito e thresholds práticos
• Recomendou experimentos de follow-up se necessário

Pesquisador/clinico

• Registrou protocolo (pre-registration)
• Planejou amostragem e critérios de exclusão
• Considerou riscos éticos ao interpretar falsos positivos

Casos de uso e heurísticas rápidas

• Heurística de tamanho amostral: para detectar um efeito pequeno com poder 80% e alpha 0,05, normalmente você precisa de centenas de observações; para efeito grande, dezenas podem bastar. Faça power analysis específica.
• Quando em dúvida, prefira testes não paramétricos se violação de normalidade for clara e amostras forem pequenas.
• Use visualização (violin, boxplot, scatter) para entender distribuição antes do teste.

Fluxo de decisão (Mermaid)

flowchart TD
  A[Começar: Defina H0/H1 e alpha] --> B{Tipo de dados}
  B -->|Numéricos contínuos| C[Verificar normalidade]
  B -->|Categorias| D[Usar qui-quadrado ou proporções]
  C -->|Normal| E{Comparação de grupos}
  C -->|Não normal| F[Considerar teste não paramétrico ou bootstrap]
  E -->|2 grupos| G{Dependentes?}
  G -->|Sim| H[t-test pareado]
  G -->|Não| I[t-test independente]
  E -->|>=3 grupos| J[ANOVA + Post-hoc]
  F --> K[Mann-Whitney / Kruskal-Wallis / Bootstrap]
  H --> L[Reportar p, effect size, IC]
  I --> L
  J --> L
  K --> L

Medidas e métricas importantes (fact box)

• Alpha comum: 0,05 (5%) e 0,01 (1%).
• Poder típico desejado: 80% (0,8) ou 90% (0,9).
• p-value: probabilidade de observar dados tão extremos sob H0.
• Tamanho do efeito: Cohen’s d, eta-squared, R².
• Correções para múltiplos testes: Bonferroni, Holm, Benjamini-Hochberg (FDR).

Boas práticas de código e reprodutibilidade

• Use notebooks com células bem comentadas e requisitos (requirements.txt).
• Fixe seeds para reprodutibilidade quando simular dados (rng = np.random.default_rng(seed)).
• Salve resultados e scripts de análise em controle de versão.

Exemplos de teste rápido

One-sample t-test:

# Exemplo completo
import numpy as np
import pingouin as pg
rng = np.random.default_rng(42)
a = rng.normal(loc=0.5, scale=1.0, size=30)
pg.ttest(a, 0.45)

Linear regression:

import seaborn as sns
import pingouin as pg
tips = sns.load_dataset('tips')
pg.linear_regression(tips['total_bill'], tips['tip']).round(3)

Teste não paramétrico (MWU):

from pingouin import mwu
a = rng.random(25)
b = rng.random(25)
mwu(a, b)

Questões éticas e privacidade

Ao lidar com dados humanos, verifique conformidade com leis locais de proteção de dados (ex.: GDPR na UE, LGPD no Brasil). Agregue e anonimiza dados quando possível; solicite consentimento informado quando aplicável.

Glossário rápido

• p-value: probabilidade dos dados observados assumindo H0.
• alpha: limiar de significância definido antes do teste.
• erro Tipo I: falso positivo.
• erro Tipo II: falso negativo.

Resumo final

Testes estatísticos em Python (NumPy, Seaborn, Pingouin) permitem validar se resultados são plausíveis além do acaso. Sempre verifique pressupostos, reporte tamanhos de efeito, planeje amostragem e proteja sua análise contra comparações múltiplas e p-hacking.

Importante: interpretação correta e contexto (impacto prático) são tão relevantes quanto significância estatística.

Notas

• Se estiver avaliando múltiplas hipóteses, aplique correções apropriadas.
• Prefira reportar intervalos de confiança e medidas de efeito junto com p-values.

Estatística em Python é rápida de aplicar, mas exige responsabilidade: bons resultados epidemiológicos, clínicos ou de negócio dependem tanto do desenho quanto da análise.