Regresión en Python: guía práctica para encontrar relaciones y predecir

Enlaces rápidos

• Simple Linear Regression: Finding Trends

• Multiple Linear Regression: Taking Regression into the Third Dimension, And Beyond

• Nonlinear Regression: Fitting Curves

• Logistic Regression: Fitting Binary Categories

Introducción: por qué usar regresión en Python

Reunir datos no basta. Puedes llenar hojas de cálculo, pero no sirven si no puedes actuar sobre ellas. La regresión es una de las herramientas estadísticas más potentes para encontrar relaciones en los datos. Python facilita el proceso y ofrece mucha más flexibilidad que una hoja de cálculo. Deja el lápiz y la regla y usa Python. Aquí verás cómo empezar, ejemplos reproducibles y prácticas recomendadas.

Importante: definir términos en una línea

• Regresión: técnica estadística para modelar la relación entre variables y, opcionalmente, predecir valores.
• Variable independiente: predictor (x).
• Variable dependiente: objetivo o respuesta (y).

Simple Linear Regression: encontrar tendencias

La regresión lineal simple modela la relación entre dos variables: una independiente (x) y otra dependiente (y). Normalmente graficamos x en el eje horizontal y y en el vertical. El objetivo es ajustar una recta que describa la relación entre los puntos.

Ejemplo práctico: propinas en restaurantes de Nueva York

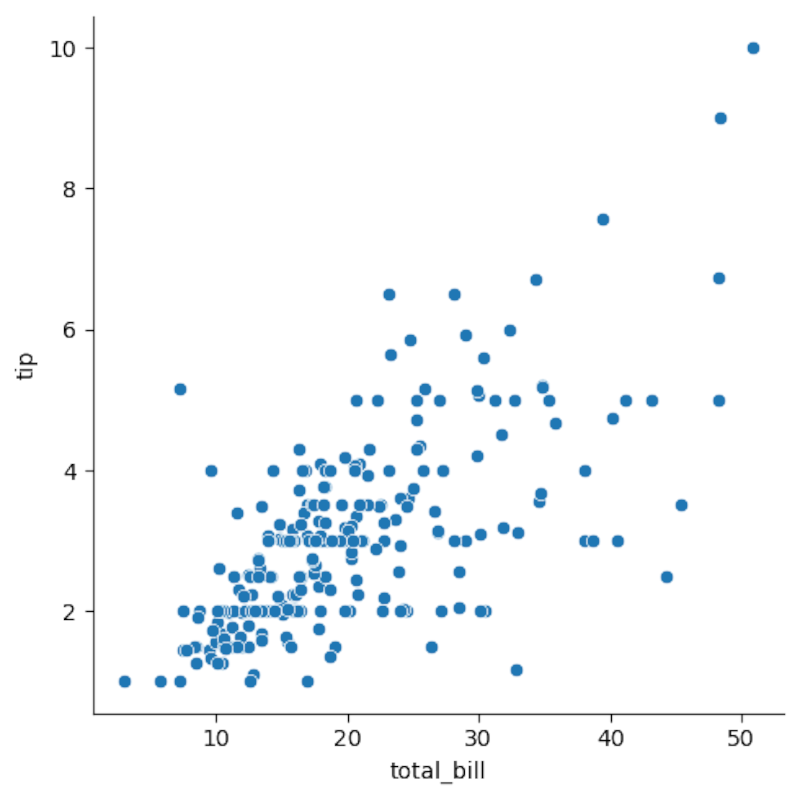
Usaremos el conjunto de datos “tips” incluido en Seaborn. Queremos saber si existe relación entre el monto total de la cuenta (total_bill) y la propina (tip).

Código de ejemplo (Seaborn y carga de datos):

import seaborn as sns

tips = sns.load_dataset('tips')

Si usas un notebook Jupyter, incluye:

%matplotlib inline

Graficamos el diagrama de dispersión con relplot:

  
sns.relplot(x='total_bill',y='tip',data=tips)

Observación: el diagrama sugiere una relación aproximadamente lineal positiva. Para visualizar la recta de regresión:

  
sns.regplot(x='total_bill',y='tip',data=tips)

Podemos realizar un análisis formal con Pingouin. Su método linear_regression calcula coeficientes y métricas de ajuste:

import pingouin as pg  
pg.linear_regression(tips['total_bill'],tips['tip']).round(2)

Puntos clave sobre la salida:

• r² indica la proporción de varianza de y explicada por x. En el ejemplo r² ≈ 0.46, un ajuste razonable para datos reales.
• La raíz de r² aproxima la correlación (r ≈ 0.68 en este caso), indicando relación positiva.

Ecuación de la recta (ejemplo):

tip = 0.11(total bill) + 0.92

Ó, escrita de forma estándar:

tip = 0.92 + 0.11 * total_bill

Función de predicción en Python (recuerda la indentación de 4 espacios):

def tip(total_bill):  
    return 0.92 + 0.11 * total_bill

Predicción sobre una cuenta de 100 USD:

  
tip(100)

Resultado esperado: aproximadamente 12 USD.

Nota: los coeficientes y la validez del modelo dependen del muestreo, outliers y supuestos (linealidad, homocedasticidad, independencia de errores).

Regresión lineal múltiple: sumar predictores

La regresión lineal se extiende a múltiples variables independientes. En lugar de ajustar una recta en 2D, ajustas un hiperplano en un espacio de dimensión mayor. Visualizarlo es más difícil, pero el proceso es similar.

Ejemplo: agregar el tamaño de la mesa (size) como predictor adicional:

  
pg.linear_regression(tips[['total_bill','size']],tips['tip']).round(2)

Observa que usamos doble corchete para pasar varias columnas.

Interpretación práctica:

• Si r² no cambia mucho respecto al modelo simple, el nuevo predictor aporta poca información adicional.
• Coeficientes indican el efecto esperado en la variable objetivo por unidad de cambio en cada predictor, con los demás predictores constantes.

Función de predicción múltiple de ejemplo:

  
def tip(total_bill,size):  
    return 0.67 + 0.09 * total_bill + 0.19 * size

Precauciones:

• Multicolinealidad: predictores correlacionados entre sí inflan la varianza de los coeficientes.
• Escalado: variables con diferentes unidades pueden necesitar estandarización.

Regresión no lineal: ajustar curvas

No todas las relaciones son lineales. Puedes ajustar polinomios, exponenciales u otras funciones. A menudo conviertes el problema a una regresión lineal sobre transformaciones de la variable (por ejemplo, x², log(x)).

Ejemplo con una parábola cuadrática generada con NumPy:

  
x = np.linspace(-100,100,1000)

y = 4*x**2 + 2*x + 3

Construimos un DataFrame con Pandas:

import pandas as pd  
df = pd.DataFrame({'x':x,'y':y})

df.head()

Scatterplot:

sns.relplot(x='x',y='y',data=df)

Ajuste de un polinomio de orden 2 con Seaborn:

sns.regplot(x='x',y='y',order=2,data=df)

También podemos crear la variable x² y usar regresión lineal clásica sobre [x, x²]:

df['x2'] = df['x']**2

pg.linear_regression(df[['x','x2']],df['y']).round(2)

En datos artificiales como este, r² = 1 indica ajuste perfecto. En datos reales rara vez verás r² exactamente 1.

Función predicción cuadrática de ejemplo:

def quad(x):  
    return 3 + 2*x + 4*x**2

Puedes extender esto a polinomios de grado mayor o a transformaciones no polinomiales, y usar técnicas de regularización si el grado es alto.

Regresión logística: categorías binarias

Para modelos cuyo objetivo es binario (por ejemplo, sobrevivió/no sobrevivió), la regresión logística modela la probabilidad de pertenecer a una clase. En vez de predecir valores continuos, predice probabilidades entre 0 y 1.

Ejemplo: ¿el precio del billete (fare) influyó en la supervivencia en el Titanic?

Carga del dataset y vista previa:

titanic = sns.load_dataset('titanic')

titanic.head()

Graficamos y forzamos un ajuste logístico con lmplot:

sns.lmplot(x='fare',y='survived',logistic=True,data=titanic)

Pingouin también ofrece regresión logística:

pg.logistic_regression(titanic['fare'],titanic['survived']).round(2)

Interpretación de salida:

• p-value (pval): indica la significancia estadística del predictor. Un valor muy bajo sugiere que el predictor aporta información sobre la variable objetivo.
• Coeficiente positivo: mayor fare→mayor probabilidad de sobrevivir (en este ejemplo).

Importante: significancia estadística no equivale a causalidad.

Buenas prácticas al aplicar regresión

1. Visualiza siempre tus datos antes de modelar. Gráficos rápidos (scatter, boxplot) detectan outliers, patrones no lineales y errores.
2. Divide datos en train/test o usa validación cruzada para evaluar generalización.
3. Revisa supuestos (linealidad, normalidad de errores, homocedasticidad) cuando aplicables.
4. Trata valores atípicos e imputación de faltantes de forma explícita.
5. Escala variables si usas regresión con regularización o cuando las unidades difieren mucho.
6. Reporta métricas relevantes: r², RMSE, AUC (para clasificación), p-values.

Casos en los que la regresión puede fallar

• Relación no monotónica o altamente no lineal que requiere otro modelo (árboles, splines, redes neuronales).
• Datos con muchos outliers que distorsionan la estimación de coeficientes.
• Multicolinealidad severa que hace que los coeficientes sean inestables.
• Pequeño tamaño de muestra que produce estimaciones poco fiables.
• Cambios en el proceso generador de datos (data drift) que invalidan modelos entrenados en el pasado.

Contraejemplos prácticos:

• Intentar ajustar una recta a una relación en forma de U sin transformar variables o usar polinomios dará malos resultados.
• Usar solo p-values para seleccionar variables puede llevar a modelos sobreajustados.

Alternativas y complementos a la regresión clásica

• Modelos de árboles (Random Forest, XGBoost) para relaciones no lineales y variables categóricas sin mucha preparación.
• Splines y modelos aditivos generalizados (GAM) para relaciones suaves no lineales.
• Redes neuronales para interacciones complejas en datos grandes.
• Métodos robustos (RANSAC, HuberRegressor) cuando hay outliers.

Decisión rápida (mental model): si la relación parece lineal y quieres interpretabilidad, usa regresión lineal. Si la prioridad es precisión sobre interpretabilidad y hay no linealidad, prueba árboles o ensambles.

Mini-metodología: pasos para aplicar regresión a tus datos

1. Definir la pregunta: qué quieres predecir y por qué.
2. Explorar datos: resumen estadístico y visualizaciones.
3. Limpiar y transformar: imputar perdidos, codificar categorías, escalar si es necesario.
4. Seleccionar características: a priori por negocio o usando técnicas (LASSO, selección hacia atrás).
5. Elegir el modelo y entrenar con validación cruzada.
6. Evaluar: métricas adecuadas y diagnóstico de residuos.
7. Documentar supuestos y limitaciones.
8. Desplegar y monitorear desempeño en producción.

Role-based checklists

Data Scientist

• Validar supuestos del modelo.
• Probar regularización y selectores de características.
• Construir pipeline reproducible y reportes.

Data Analyst

• Generar visualizaciones claras.
• Comunicar interpretación de coeficientes para stakeholders.
• Preparar dataset limpio y etiquetado.

Data Engineer

• Automatizar pipelines de ingestión y transformación.
• Asegurar versionado de datos y modelos.
• Monitorizar latencia y disponibilidad del modelo en producción.

Ejemplos de test cases y criterios de aceptación

• El modelo debe superar el baseline (p. ej. predicción por media) en RMSE o AUC.
• Las predicciones deben estar dentro de rangos plausibles y no generar NaN.
• Un conjunto de validación simulado no debe mostrar fuerte degradación (>10% en métricas) respecto al conjunto de entrenamiento.

Mapa de decisiones simple (Mermaid)

flowchart TD
  A[¿Variable objetivo continua?] -->|Sí| B{¿Relación lineal visible?}
  A -->|No| C[Clasificación: usar regresión logística u otro clasificador]
  B -->|Sí| D[Regresión lineal / lineal múltiple]
  B -->|No| E{¿Curva suave/no lineal?}
  E -->|Sí| F[Polinomios o GAM]
  E -->|No| G[Modelos no lineales: árboles / ensambles / NN]

Mapa de madurez rápido (heurística)

• Nivel 1 — Exploratorio: visualizaciones y modelos simples.
• Nivel 2 — Reproducible: pipelines y validación cruzada.
• Nivel 3 — Productivo: despliegue, monitoreo y reentrenamiento.

Seguridad y privacidad

• Minimiza el uso de datos sensibles en modelos. Anonimiza o agrega privacidad diferencial cuando sea necesario.
• Controla accesos a datasets que contengan información personal.
• Documenta qué columnas son PII/PCI y elimina o protege antes del análisis.

Notas sobre GDPR y datos personales: si trabajas con datos de residentes en la UE, asegúrate de tener bases legales claras para el procesamiento y, cuando corresponda, ejecuta evaluaciones de impacto y mecanismos de consentimiento.

Compatibilidad y migración

• Pingouin y Seaborn funcionan con versiones recientes de Pandas y NumPy. Mantén tu entorno virtual controlado (conda/mamba/venv) y registra versiones en un requirements.txt o environment.yml.
• Para producción, considera convertir el modelo a formatos portables (ONNX, PMML) o empaquetarlo como servicio REST.

Edge-cases y recomendaciones prácticas

• Outliers extremos: verifica y decide si eliminarlos, winsorizar o usar modelos robustos.
• Observaciones con valores faltantes: evita eliminar filas en bloque si reducen mucho el dataset; usa imputación.
• Variables categóricas con muchas categorías: agrupa niveles infrecuentes o usa embeddings en modelos complejos.

Pequeño glosario de línea

• r²: fracción de la varianza explicada por el modelo.
• RMSE: raíz del error cuadrático medio; mide error en unidades de la variable objetivo.
• AUC: área bajo la curva ROC; mide capacidad discriminativa en clasificación.

Resumen final

• La regresión en Python es versátil y accesible gracias a bibliotecas como Seaborn, Pingouin, NumPy y Pandas.
• Visualiza datos primero, selecciona el modelo por la forma de la relación y valida con datos no vistos.
• Considera alternativas cuando la relación no sea lineal o los datos presenten outliers o multicolinealidad.

Importante: las métricas y la validez del modelo dependen mucho de la calidad de los datos y del cumplimiento de supuestos; documenta siempre limitaciones y supuestos.

Si quieres, puedo convertir cualquiera de los ejemplos en un notebook reproducible, preparar un pipeline básico (data cleaning → entrenamiento → evaluación) o ayudarte a elegir entre modelos según tu dataset. Indica el tamaño de tu conjunto de datos, las columnas principales y el objetivo que buscas predecir.