Pruebas estadísticas en Python: guía práctica

Actualización: 27/09/2025 10:54 EST por David Delony — Una versión anterior mezcló las definiciones de falsos positivos y falsos negativos. Un error de Tipo I es un falso positivo; un error de Tipo II es un falso negativo.

Índice

• Qué es la prueba de hipótesis
• Por qué usar pruebas estadísticas
• Significado estadístico vs. práctico
• Student’s t-test (prueba t)
• Regresión lineal y prueba del coeficiente
• ANOVA
• Pruebas no paramétricas
• Alternativas: métodos bayesianos y re-muestreo
• Cuándo fallan las pruebas estadísticas (limitaciones comunes)
• Mini-metodología: pasos recomendados
• Heurísticas y modelos mentales
• Diagrama para elegir una prueba (Mermaid)
• Listas de verificación por rol
• Glosario rápido
• Resumen y recomendaciones finales

Qué es la prueba de hipótesis

La prueba de hipótesis es una metodología estadística para decidir si los resultados observados en una muestra son compatibles con una afirmación previa (hipótesis nula) o si aportan evidencia suficiente para preferir una hipótesis alternativa. En una línea: la prueba cuantifica cuán improbable sería observar tus datos si la hipótesis nula fuera cierta.

Definiciones en una línea:

• Hipótesis nula (H0): la suposición base que normalmente indica ausencia de efecto.
• Hipótesis alternativa (H1): lo que quieres probar (por ejemplo, diferencia, relación).
• Nivel de significancia (alpha): probabilidad tolerada de cometer un error Tipo I (rechazar H0 siendo verdadera).
• p-valor: probabilidad de obtener datos tan extremos como los observados si H0 fuera cierta.
• Error Tipo I: falso positivo (rechazas H0 cuando es verdadera).
• Error Tipo II: falso negativo (no rechazas H0 cuando H1 es verdadera).
• Tamaño del efecto: magnitud práctica de la diferencia o relación (complemento esencial al p-valor).

Importante: determina H0, H1 y alpha antes de mirar los resultados. Predefine también la estadística que usarás y un plan para comprobación de supuestos.

Por qué usar pruebas estadísticas

Las cifras por sí solas pueden engañar. Dos medias pueden diferir, pero la diferencia puede deberse al azar por el tamaño muestral o a la variabilidad. Las pruebas estadísticas nos dan una medida formal —el p-valor— para decidir si la diferencia es improbable bajo H0.

Casos de uso típicos:

• Ensayos clínicos: ¿el fármaco reduce la presión arterial más que el placebo?
• Experimentos de producto: ¿aumenta una nueva interfaz la tasa de conversión?
• Investigación académica: ¿difieren las medias entre grupos tratados?

Las pruebas no sustituyen el pensamiento crítico. Además del p-valor debes reportar estimaciones (p. ej., medias), intervalos de confianza y tamaños del efecto.

Significado estadístico vs. práctico

Un resultado puede ser estadísticamente significativo (p < alpha) y no ser relevante en la práctica si el efecto es minúsculo. A la inversa, un efecto grande con baja potencia (p > alpha) puede pasar desapercibido.

Consejos:

• Siempre reporta tamaño del efecto y CI junto al p-valor.
• Considera la importancia clínica/comercial antes de concluir.
• Usa tamaño de muestra/poder estadístico para planificar estudios.

Student’s t-test

La prueba t de Student compara medias cuando los datos parecen seguir una distribución aproximadamente normal y las varianzas entre grupos son razonablemente similares. Es la elección clásica cuando trabajas con muestras pequeñas y desconoces la desviación estándar poblacional.

Ejemplo paso a paso con Python (Pingouin + NumPy):

1. Generar una muestra aleatoria de la distribución normal.

import numpy as np
rng = np.random.default_rng()

2. Crear un vector de 15 observaciones desde una normal estándar:

a = rng.standard_normal(15)

3. Comprobar normalidad (Shapiro-Wilk) con Pingouin:

import pingouin as pg
pg.normality(a)

Interpretación: la función devuelve la estadística de Shapiro y el p-valor. Si p > 0.05 no hay evidencia fuerte para rechazar normalidad en muestras pequeñas; si p < 0.05 hay indicios de no normalidad y conviene usar pruebas no paramétricas o re-muestreo.

4. Probar si la media difiere de 0.45:

pg.ttest(a, .45)

Si el p-valor es 0.99 no rechazas H0; la diferencia observada puede explicarse por azar.

Limitaciones de la t:

• Sensible a outliers.
• Supone normalidad (especialmente con n pequeño).
• Si las varianzas entre grupos difieren mucho, usa la versión de Welch o alternativas.

Regresión lineal

La regresión lineal ajusta una recta a una nube de puntos y permite evaluar si existe asociación entre una variable predictora y otra respuesta. La prueba estadística típica para regresión evalúa si la pendiente es distinta de cero.

Ejemplo con Seaborn y Pingouin usando el dataset de tips:

import seaborn as sns
tips = sns.load_dataset('tips')

Explora el DataFrame:

tips.head()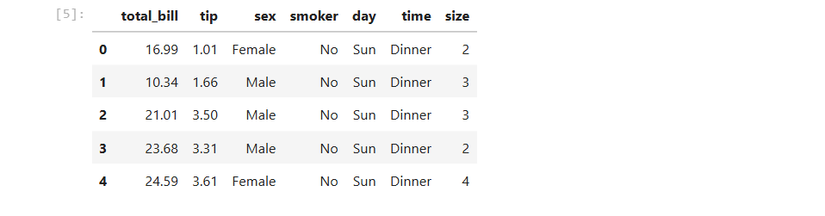

Dibuja una regresión simple:

sns.regplot(x='total_bill', y='tip', data=tips)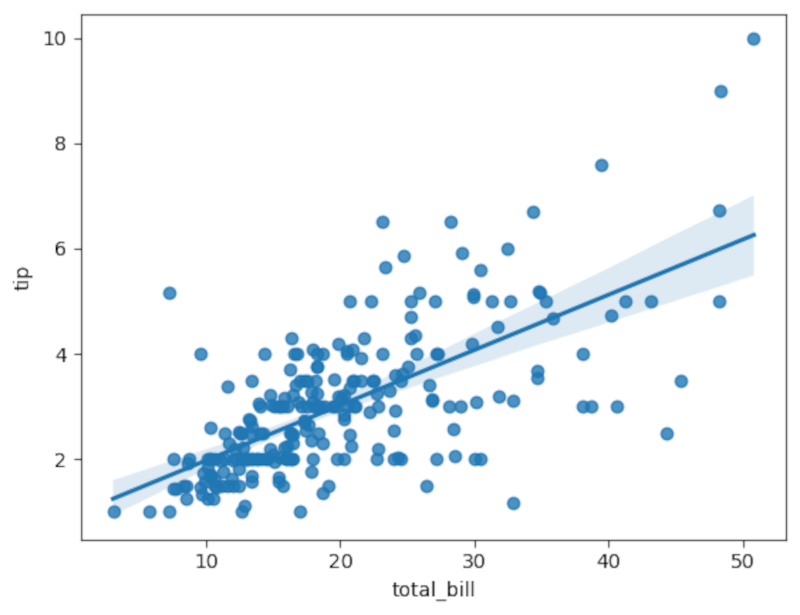

Para un análisis más formal usa pingouin.linear_regression, que devuelve coeficientes, errores estándar, t-values y p-valores:

pg.linear_regression(tips['tip'], tips['total_bill']).round(2)

Interpretación: un t-valor grande en valor absoluto y un p-valor muy pequeño indican que la pendiente difiere significativamente de cero. Aún así, evalúa R² y residuales para comprobar el ajuste. Un p-valor pequeño no implica que la relación sea fuerte: puede deberse a gran tamaño muestral.

Consejos prácticos para regresión:

• Visualiza residuales.
• Comprueba homocedasticidad (varianza constante).
• Comprueba independencia de observaciones.
• Considera transformaciones o modelos robustos si hay outliers o heterocedasticidad.

ANOVA

ANOVA (Analysis of Variance) compara medias entre tres o más grupos. La idea es comparar la variabilidad entre grupos con la variabilidad dentro de los grupos. Si la variabilidad entre grupos es mucho mayor que la interna, es probable que exista una diferencia real entre al menos dos grupos.

Ejemplo con pingouin y el dataset de pingüinos:

penguins = pg.read_dataset('penguins')
pg.anova(data=penguins, dv='flipper_length_mm', between='species').round(2)

Si el p-valor sale cercano a 0.0 rechazas la hipótesis nula de medias iguales entre especies. ANOVA te dice si existe al menos una diferencia significativa, pero no qué grupos difieren. Para comparar pares usa pruebas post-hoc (Tukey, Bonferroni) o comparaciones por pares ajustando alpha.

Puntos clave:

• Revisa supuestos: normalidad por grupo y homogeneidad de varianzas.
• Para variancias desiguales usa Welch ANOVA o métodos no paramétricos.
• Acompaña el resultado con tamaños de efecto (eta², omega²).

Pruebas no paramétricas

Cuando los datos no cumplen supuestos (normalidad, varianzas iguales) las pruebas no paramétricas son alternativas robustas porque no asumen una distribución específica.

Ejemplos con Pingouin:

Mann–Whitney U (contrasta dos grupos independientes):

a = rng.random(15)
b = rng.random(15)
pg.mwu(a, b)

Kruskal–Wallis (equivalente no paramétrico a ANOVA para 3+ grupos):

pg.kruskal(data=penguins, dv='flipper_length_mm', between='species').round(2)

Interpretación: estas pruebas trabajan con rangos y mediana relativa. Ofrecen una alternativa cuando la normalidad falla, pero también tienen limitaciones: pierden potencia si los datos sí fueran normales y no corrigen por efectos de covariables.

Alternativas y enfoques modernos

No estás restringido a las pruebas clásicas. Algunas alternativas útiles:

• Bootstrap y re-muestreo: construye intervalos de confianza empíricos para medias, diferencias o coeficientes sin asumir normalidad.
• Tests de permutación: evalúan la significancia mediante reordenamientos aleatorios de etiquetas.
• Métodos bayesianos: estiman distribuciones a posteriori de parámetros y permiten cuantificar la probabilidad de hipótesis.
• Modelos robustos y regresión cuantílica: reducen sensibilidad a outliers.

Cuando usar cada uno:

• Usar bootstrap si dudas de supuestos y quieres intervalos robustos.
• Usar permutación si la hipótesis nula implica intercambio aleatorio de etiquetas.
• Usar bayesiano si prefieres probabilidades explícitas sobre parámetros y puedes especificar prior.

Cuándo fallan las pruebas estadísticas (limitaciones comunes)

1. Supuestos rotos. Muchas pruebas requieren normalidad, independencia y homocedasticidad. Si no se cumplen, el p-valor puede ser engañoso.
2. Tamaño muestral inadecuado. Poca muestra → baja potencia; muestra gigantesca → detecta diferencias triviales.
3. Multiplicidad. Ejecutar muchas pruebas sin corrección (p-hacking) aumenta falsos positivos.
4. Confusión entre asociación y causalidad. Una relación estadística no implica causalidad sin diseño o análisis causal.
5. Ignorar tamaño del efecto e intervalos de confianza. El p-valor no informa magnitud.

Mitigaciones:

• Pre-registra el análisis cuando sea posible.
• Ajusta por múltiples comparaciones (Bonferroni, Holm, FDR).
• Calcula y reporta tamaños del efecto y CI.
• Aumenta muestra si la potencia es baja; haz análisis de poder previo.

Mini-metodología: pasos recomendados antes y durante el análisis

1. Define la pregunta y las hipótesis (H0 y H1).
2. Escoge la medida principal y el nivel alpha (p. ej., 0.05).
3. Calcula tamaño de muestra / poder estadístico (si es posible).
4. Explora y limpia datos; identifica outliers y patrones faltantes.
5. Verifica supuestos (normalidad, varianza, independencia).
6. Elige la prueba apropiada (paramétrica vs no paramétrica) y documenta la elección.
7. Ejecuta la prueba, calcula p-valor, tamaño del efecto y CI.
8. Ajusta por comparaciones múltiples si aplicable.
9. Interpreta resultados en contexto práctico, no solo estadístico.
10. Documenta todo: datos, código, versión de librerías, decisiones y resultados.

Plantilla de reporte mínimo:

• Pregunta y diseño del estudio.
• Hipótesis H0/H1 y alpha.
• Tamaño muestral y cálculo de poder (si existe).
• Prueba utilizada y comprobación de supuestos.
• Estadística principal, p-valor, tamaño del efecto y CI.
• Conclusión práctica.

Heurísticas y modelos mentales

• Piensa en la hipótesis nula como una suposición que buscas falsar.
• El p-valor no mide la probabilidad de H0; mide la improbabilidad de los datos bajo H0.
• Usa el tamaño del efecto para juzgar relevancia práctica.
• A mayor ruido y menor efecto, mayor muestra necesitas para detectar diferencias.
• Si aplicas muchas comparaciones, ajusta el umbral o controla la tasa de falsos descubrimientos.

Diagrama de decisión: elegir una prueba

flowchart TD
  A[¿Comparas medias o buscas asociación?] -->|Medias| B{¿Número de grupos}
  B -->|1 muestra| C[Prueba t de una muestra]
  B -->|2 grupos| D{¿Independientes?}
  D -->|Sí| E{¿Datos normales?}
  E -->|Sí| F[Prueba t independiente]
  E -->|No| G[Mann-Whitney U]
  D -->|No 'pareados'| H[Prueba t pareada o Wilcoxon firmado]
  B -->|3+ grupos| I{¿Datos normales y varianzas iguales?}
  I -->|Sí| J[ANOVA]
  I -->|No| K[Kruskal-Wallis]
  A -->|Asociación/Regresión| L{¿Variable dependiente continua?}
  L -->|Sí| M[Regresión lineal; comprobar supuestos]
  L -->|No 'categoría'| N[Regresión logística]
  style G fill:#f9f,stroke:#333,stroke-width:1px

Listas de verificación por rol

Data scientist / analista:

• Reproducibilidad: incluye script, semilla aleatoria y versiones de paquetes.
• Chequeo de supuestos y diagnóstico de residuales.
• Reporta p-valores, tamaños de efecto e IC.
• Guarda resultados intermedios y decisiones de limpieza.

Investigador / científico:

• Pre-registra hipótesis y plan de análisis si es posible.
• Plan de tamaño muestral basado en mínima diferencia relevante.
• Interpreta resultados en contexto clínico/teórico.

Product manager / stakeholder:

• Exige interpretación en términos de impacto (lift %, cambios absolutos).
• Pide métricas de confianza: intervalos y tamaño del efecto.
• Solicita validación con datos fuera de muestra si es aplicable.

Revisor / auditor:

• Verifica correcciones por multiplicidad.
• Comprueba la existencia de análisis exploratorios ocultos.
• Contrasta conclusiones con la magnitud práctica del efecto.

Glosario (una línea cada término)

• p-valor: probabilidad de observar datos tan extremos bajo H0.
• Alpha: umbral para rechazar H0 (p.ej., 0.05).
• Tamaño del efecto: medida de la magnitud de una diferencia o asociación.
• Potencia: probabilidad de detectar un efecto real dado un tamaño y alpha.
• Bootstrapping: técnica de re-muestreo para estimar incertidumbre sin asumir distribución.

Buenas prácticas de reporte

• No te limites al p-valor. Incluye estimaciones y CI.
• Publica código y datos cuando sea posible y compatible con la privacidad.
• Ajusta por comparaciones múltiples y reporta el método usado.
• Evita lenguaje absoluto: habla en términos de evidencia (p. ej., “evidencia sólida a favor de…”).

Ejemplo de interpretación (cómo comunicar resultados)

Malo: “El test dio p = 0.03, por lo tanto funciona.”

Bueno: “La prueba t da p = 0.03, lo que sugiere que la diferencia observada es improbable bajo la hipótesis nula (alpha = 0.05). La diferencia media fue de 1.2 unidades (IC 95%: 0.3–2.1), lo que indica un tamaño del efecto pequeño-moderado y un posible impacto práctico moderado en el contexto del estudio.”

Notas sobre privacidad y ética

• En experimentos con datos personales, anonimiza y minimiza antes del análisis.
• Evita publicar datos que permitan reidentificación.
• Si trabajas con ensayos clínicos o datos sensibles, sigue las regulaciones locales y protocolos de aprobación ética.

Resumen y recomendaciones finales

• Las pruebas estadísticas convierten observaciones en evidencia cuantificable.
• Define H0/H1 y alpha antes de analizar.
• Comprueba supuestos y elige pruebas no paramétricas o métodos de re-muestreo si estos fallan.
• Reporta p-valores, tamaños de efecto e intervalos de confianza.
• Complementa pruebas clásicas con enfoques modernos (bootstrap, bayesiano) cuando convenga.

Importante: una buena práctica clave es documentar y automatizar el flujo de trabajo (código, datos y decisiones). Esto facilita la revisión, la reproducción y la confianza en tus conclusiones.

Resumen corto: Las pruebas estadísticas en Python son accesibles y potentes. Con bibliotecas modernas puedes comprobar supuestos, ejecutar pruebas paramétricas y no paramétricas, y reforzar conclusiones con bootstrap o enfoques bayesianos. No olvides interpretar resultados en contexto y reportar tamaños de efecto.