Hypothesentests in Python: Praktischer Leitfaden

Hypothesentests helfen zu entscheiden, ob beobachtete Unterschiede in Daten zufällig sind oder eine echte Wirkung anzeigen. Dieser Leitfaden erklärt Konzepte wie p-Wert, Alpha, Fehler 1. und 2. Art, zeigt Praxisbeispiele in Python mit Pingouin, Seaborn und NumPy und liefert Playbooks, Checklisten und Alternativen wie Bootstrap und Bayessche Tests.

Update lesen

• Eine frühere Version dieses Artikels hat die Definitionen von False Positives und False Negatives vertauscht. Ein Fehler 1. Art ist ein False Positive, ein Fehler 2. Art ist ein False Negative. Diese Korrektur wurde am 27.09.2025 vorgenommen.

Sprungmarken

• Was ist ein Hypothesentest?
• Warum statistische Tests?
• Student-t-Test
• Lineare Regression
• ANOVA
• Nichtparametrische Tests
• Praxis-Playbook: Hypothesentest in Python
• Wann Tests scheitern
• Alternative Ansätze
• Entscheidungsbaum für die Testauswahl
• Rollen- und Akzeptanzchecklisten
• Faktenbox und Glossar
• FAQ

Einleitung

Daten ohne Kontext sind nur Zahlen. Hypothesentests geben Ihnen eine strukturierte Methode, um zu prüfen, ob Unterschiede, Zusammenhänge oder Effekte in Ihren Daten statistisch bedeutsam sind. Die Tests verwandeln Beobachtungen in informierte Entscheidungen. Dieser Leitfaden kombiniert Theorie, konkrete Python-Beispiele und umsetzbare Checklisten für die Praxis.

Was ist ein Hypothesentest?

Ein Hypothesentest ist eine standardisierte Vorgehensweise in der Statistik, um zu prüfen, ob eine Beobachtung mit Zufall vereinbar ist. Kurz gesagt: Er beantwortet die Frage „Könnte dieses Ergebnis rein zufällig entstanden sein?“

Kernbegriffe in einer Zeile

• Nullhypothese (H0): Annahme, dass kein Effekt vorliegt.
• Alternativhypothese (H1): Annahme, dass ein Effekt existiert.
• Signifikanzniveau (Alpha): Fehlertoleranz für einen Fehler 1. Art (üblich: 0,05 oder 0,01).
• p-Wert: Wahrscheinlichkeit, das beobachtete Ergebnis (oder extremer) zu bekommen, wenn H0 wahr ist.
• Fehler 1. Art: H0 ablehnen, obwohl sie wahr ist (False Positive).
• Fehler 2. Art: H0 nicht ablehnen, obwohl sie falsch ist (False Negative).

Wichtig: Legen Sie H0, H1 und Alpha immer vor der Auswertung fest. So vermeiden Sie unbeabsichtigte Verzerrungen.

Warum statistische Tests?

Statistische Tests geben eine gemeinsame Sprache, um Evidenz zu quantifizieren. Sie helfen,\n

• zufällige Schwankungen von echten Effekten zu unterscheiden,
• Ergebnisse nachvollziehbar zu kommunizieren,
• Entscheidungen zu begründen (z. B. Arzneimittelzulassung, A/B-Tests).

Tests sind kein Ersatz für kritisches Denken. Sie sind Werkzeuge, die Hypothesen stützen oder widerlegen können, wenn man Annahmen überprüft und Grenzen kennt.

Student-t-Test

Der Student-t-Test vergleicht Mittelwerte. Er ist sinnvoll, wenn die zugrunde liegende Verteilung annähernd normal ist und die Varianzen kompatibel.

Wann nutzen?

• Ein Stichprobenmittel gegen einen Referenzwert testen.
• Zwei unabhängige Stichproben auf gleichen Mittelwert testen.

Beispiel mit Python: NumPy und Pingouin

Zuerst NumPy importieren und einen Zufallszahlengenerator initialisieren:

import numpy as np
rng = np.random.default_rng()

Erzeuge eine Stichprobe mit 15 Werten aus der Standardnormalverteilung:

a = rng.standard_normal(15)

Vor dem t-Test prüfen wir die Normalität mit dem Shapiro-Wilk-Test (Pingouin bietet eine bequeme Schnittstelle):

import pingouin as pg
pg.normality(a)

Bild: Pingouin-Normalitätstest eines Arrays

Jetzt testen wir die Nullhypothese, dass der Mittelwert der Stichprobe gleich 0,45 ist:

pg.ttest(a, .45)

Interpretation

• Ist der p-Wert < Alpha, lehnen wir H0 ab.
• In diesem simulierten Beispiel war der p-Wert ≈ 0.99. H0 lässt sich nicht ablehnen.

Grenzen des t-Tests

• Sensitiv gegenüber starken Ausreißern.
• Funktioniert gut für kleine Stichproben, wenn die Normalitätsannahme erfüllt ist.

Lineare Regression

Regression quantifiziert Zusammenhänge zwischen Variablen. Ein elementarer Test ist die Prüfung, ob die Steigung der Regressionsgeraden signifikant von 0 abweicht.

Beispiel: Seaborn-Datensatz “tips” aus New York

import seaborn as sns
tips = sns.load_dataset('tips')

Datenstruktur anschauen:

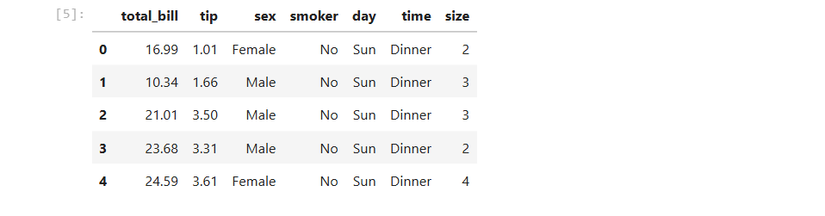
tips.head()

Bild: Ausgabe von tips.head() in Jupyter

Visualisierung mit Regressionsgerade:

sns.regplot(x='total_bill', y='tip', data=tips)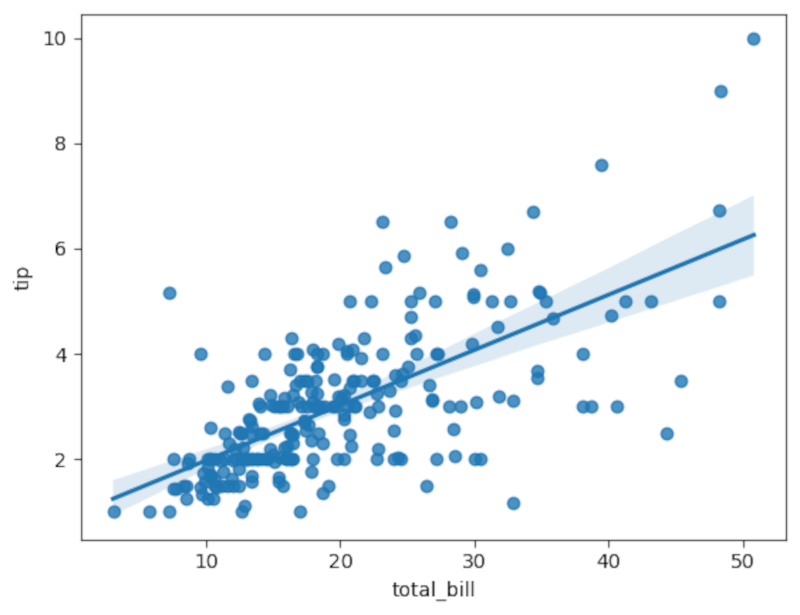

Formale Regression mit Pingouin:

pg.linear_regression(tips['tip'], tips['total_bill']).round(2)

Wichtige Punkte

• Pingouin liefert t-Statistik und p-Wert für die Steigung.
• Ein sehr kleiner p-Wert (z. B. 0.0 im Ausgabeformat) zeigt starke Evidenz gegen H0.

ANOVA

ANOVA prüft, ob Gruppenmittelwerte unterschiedlich sind. Statt paarweiser t-Tests vergleicht ANOVA mehrere Gruppen gleichzeitig und kontrolliert den Gesamttyp-I-Fehler.

Beispiel mit Pinguins-Flossenlänge:

penguins = pg.read_dataset('penguins')
pg.anova(data=penguins, dv='flipper_length_mm', between='species').round(2)

Ergebnis: p-Wert so klein, dass H0 abgelehnt werden kann. Die Spezies sagt etwas über Flossenlänge aus.

Nichtparametrische Tests

Wenn Datenverteilungen starke Abweichungen von Normalität zeigen, sind nichtparametrische Tests eine robuste Alternative.

• Mann-Whitney-U-Test: nichtparametrisches Gegenstück zum t-Test.
• Kruskal-Wallis-Test: nichtparametrische Version der ANOVA.

Beispiel Mann-Whitney-U mit zufälligen Daten:

a = rng.random(15)
b = rng.random(15)
pg.mwu(a, b)

Kruskal-Wallis für Pinguine:

pg.kruskal(data=penguins, dv='flipper_length_mm', between='species').round(2)

Nichtparametrische Tests vergleichen Ränge statt Rohwerte. Sie sind robuster gegenüber Ausreißern und Verteilungsproblemen.

Praxis-Playbook: Hypothesentest in Python

Kurzbeschreibung: Eine wiederholbare Abfolge, um Hypothesentests sauber und dokumentiert durchzuführen.

Schritt-für-Schritt

1. Formulieren Sie H0 und H1 schriftlich.
2. Definieren Sie Alpha (z. B. 0,05) und die gewünschte Teststärke.
3. Explorative Datenanalyse: Visualisieren Sie Verteilungen, Boxplots und Scatterplots.
4. Prüfen Sie Annahmen (Normalität, Varianzhomogenität, Unabhängigkeit).
5. Wählen Sie den passenden Test (t, ANOVA, Regression, Mann-Whitney, Kruskal-Wallis).
6. Führen Sie den Test in einem reproduzierbaren Notebook aus und speichern Sie Versionen.
7. Interpretieren Sie den p-Wert zusammen mit Effektgrößen und Konfidenzintervallen.
8. Dokumentieren Sie Entscheidungen, inkl. Vorregistrierung, falls nötig.
9. Sensitivitätsanalyse: Prüfen Sie Robustheit gegenüber Ausreißern oder alternativen Methoden.
10. Prüfen Sie praktische Relevanz, nicht nur statistische Signifikanz.

Playbook-Beispielcode

# 1. Daten laden
import seaborn as sns
import pingouin as pg
import numpy as np
from matplotlib import pyplot as plt

# 2. Explorative Analyse
tips = sns.load_dataset('tips')
sns.histplot(tips['total_bill'])
plt.show()

# 3. Test der Annahmen
pg.normality(tips['total_bill'])

# 4. Regressionsanalyse
res = pg.linear_regression(tips['tip'], tips['total_bill'])
print(res.round(3))

Kriterien für Akzeptanz

• p-Wert < Alpha (statistisch signifikant) UND
• Effektgröße praktisch relevant (z. B. Cohen’s d, R²) UND
• Annahmen nicht massiv verletzt oder Ergebnisse robust gegenüber Alternativen.

Wann Tests scheitern

Häufige Gründe

• Zu kleine Stichproben führen zu geringer Teststärke.
• Verletzte Annahmen (z. B. starke Schiefe, Ausreißer).
• Mehrfachtests ohne Korrektur erhöhen Fehler 1. Art.
• p-Hacking: Hypothesen nachträglich an Daten anpassen.

Counterexamples

• Große Stichproben können sehr kleine Effekte als signifikant erscheinen lassen, obwohl sie praktisch irrelevant sind.
• Nichtparametrische Tests können weniger leistungsfähig sein, wenn die Verteilung tatsächlich normal ist.

Alternative Ansätze

Wenn herkömmliche Tests nicht passen, prüfen Sie:

• Bootstrap-Methoden: Resampling zur Schätzung von Konfidenzintervallen ohne strenge Verteilungsannahmen.
• Permutationstests: Nullverteilung durch zufällige Neuverteilung der Labels erzeugen.
• Bayessche Tests: Geben direkt die Wahrscheinlichkeit von Hypothesen, nicht nur p-Werte.
• Effektgrößen-Fokus: Konzentrieren Sie sich auf praktische Relevanz und Konfidenzintervalle.

Beispiel: Bootstrap für Mittelwertdifferenz

def bootstrap_mean_diff(x, y, n_resamples=10000, rng=None):
    rng = rng or np.random.default_rng()
    diffs = []
    for _ in range(n_resamples):
        xs = rng.choice(x, size=len(x), replace=True)
        ys = rng.choice(y, size=len(y), replace=True)
        diffs.append(xs.mean() - ys.mean())
    diffs = np.array(diffs)
    return np.percentile(diffs, [2.5, 97.5])

Entscheidungsbaum für die Testauswahl

flowchart TD
  A[Start: Ziel definieren] --> B{Vergleich oder Zusammenhang?}
  B --> |Vergleich von Mittelwerten| C{Anzahl Gruppen}
  C --> |1 Gruppe| D[t-Test gegen Referenz]
  C --> |2 Gruppen| E[Unabhängiger t-Test oder Mann-Whitney]
  C --> |>2 Gruppen| F[ANOVA oder Kruskal-Wallis]
  B --> |Zusammenhang| G{Beide Variablen numerisch?}
  G --> |Ja| H[Regression]
  G --> |Nein| I[Kontingenzanalyse oder Rangkorrelation]
  D --> J[Prüfe Normalität]
  E --> J
  F --> J
  J --> K{Normal?}
  K --> |Ja| L[Parametrischer Test]
  K --> |Nein| M[Nichtparametrischer Test oder Bootstrap]
  L --> N[Ergebnis interpretieren: p-Wert, Effektgröße]
  M --> N

Rollen- und Akzeptanzchecklisten

Forscher / Data Scientist

• Hypothese vorab formuliert und dokumentiert.
• Signifikanzniveau begründet.
• Code und Daten versioniert und reproduzierbar.
• Sensitivitätsanalysen durchgeführt.

Produktmanager / Stakeholder

• Akzeptanzkriterien klar (metrische Relevanz, Mindest-Effektgröße).
• Verständnis für p-Wert und Konfidenzintervalle vorhanden.
• Entscheidungen nicht nur nach Signifikanz treffen.

Statistiker / Reviewer

• Annahmen geprüft (Normalität, Homoskedastizität, Unabhängigkeit).
• Korrekturen bei multiplen Tests empfohlen (Bonferroni, FDR).
• Effektgrößen und praktische Relevanz angefordert.

Faktenbox: Wichtige Zahlen und Faustregeln

• Alpha (häufig): 0,05 (95 % Konfidenz) oder 0,01 (99 % Konfidenz).
• Faustregel Mindeststichprobengröße: mind. 20–30 pro Gruppe für viele Tests; variiert je nach Effektgröße.
• Cohen’s d: 0,2 (klein), 0,5 (mittel), 0,8 (groß).
• Bei Mehrfachtests: Bonferroni-Korrektur = Alpha / Anzahl Tests.

Metriken und Reporting

Gute Praxis beim Reporting

• Nennen Sie p-Wert und Effektgröße.
• Geben Sie Konfidenzintervalle an.
• Beschreiben Sie Datenquelle, Filter und Preprocessing.
• Führen Sie Sensitivitätsanalysen an (Robustheit gegenüber Ausreißern).

Risiken und Gegenmaßnahmen

Risiken

• Fehler 1. Art (False Positive): Folge ist unrealistischer Glaube an einen Effekt.
• Fehler 2. Art (False Negative): Folge ist verpasste Entdeckung eines realen Effekts.
• Datenleckage oder unbeabsichtigtes Label-Snooping.

Gegenmaßnahmen

• Größere Stichprobe planen.
• Vorregistrierung von Hypothesen.
• Korrekturen für multiple Tests.
• Saubere Trennung von Trainings-, Validierungs- und Testdaten.

Datenschutz- und Compliance-Hinweise

• Verwenden Sie nur anonymisierte oder pseudonymisierte Daten, wenn personenbezogene Daten betroffen sind.
• Dokumentieren Sie Einwilligungen und Zweck der Datennutzung.
• Bei medizinischen oder persönlichen Daten prüfen Sie lokale Gesetze und GDPR-Anforderungen.

Glossar in einer Zeile

• Alpha: Signifikanzniveau. - p-Wert: Wahrscheinlichkeit unter H0. - Effektgröße: Maß für Stärke des Effekts. - Konfidenzintervall: Bereich plausibler Werte für einen Parameter.

Kurze Ankündigungsversion (100–200 Wörter)

Hypothesentests helfen zu prüfen, ob beobachtete Effekte in Daten zufällig sind oder real. Dieser Leitfaden erklärt Grundlagen wie Nullhypothese, p-Wert, Fehler 1. und 2. Art und zeigt praktische Python-Beispiele mit Pingouin, NumPy und Seaborn. Er bietet ein wiederholbares Playbook, Entscheidungsbäume für die Testauswahl, Alternativen wie Bootstrap und Bayessche Ansätze sowie Rollen- und Akzeptanzchecklisten. Zusätzlich finden Sie Hinweise zu Reporting, Datenschutz und typischen Fallstricken. Ziel ist es, den Weg von der Fragestellung zur fundierten Entscheidung reproduzierbar und transparent zu gestalten.

FAQ

Frage: Was bedeutet ein p-Wert von 0,03?

Antwort: Wenn Alpha 0,05 ist, weist ein p-Wert von 0,03 darauf hin, dass das beobachtete Ergebnis unter H0 eher unwahrscheinlich ist. Man lehnt H0 ab. Beurteilen Sie zusätzlich Effektgröße und praktische Relevanz.

Frage: Wann nutze ich einen nichtparametrischen Test?

Antwort: Wenn die Verteilung stark schief ist, Ausreißer dominieren oder Annahmen für parametrische Tests verletzt sind.

Frage: Sagt ein signifikanter Test, dass etwas nützlich ist?

Antwort: Nein. Signifikanz sagt nur, dass ein Effekt statistisch nachweisbar ist. Ob der Effekt praktisch relevant ist, beschreibt die Effektgröße und der Kontext.

Schlusswort

Hypothesentests sind mächtige Werkzeuge, aber kein Allheilmittel. Verwenden Sie sie zusammen mit guter Forschungspraxis: klare Hypothesen, dokumentierte Entscheidungen, robuste Analysen und transparente Berichte. So werden Ihre Ergebnisse belastbar und aussagekräftig.