Octaveで学ぶ信号の加算と乗算

はじめに

前回のチュートリアルでは、音声ファイルの読み書きや再生、コサイン関数からの音声合成を扱いました。本稿では信号同士の加算、乗算（変調）、および基本的な数学的操作が元の信号へ与える影響を観察します。これらの基本操作はスペクトル解析や振幅変調、角変調など高度な処理の基礎です。

信号の加算

2つの信号 S1(t) と S2(t) の和は、任意の時刻における各信号の値の和として得られる信号 R(t) です。

R(t) = S1(t) + S2(t)

以下ではOctaveで異なる周波数の2つの信号を生成し、その和をグラフと音で確認します。

手順 1: 異なる周波数の2つの信号を作成（oggファイル）

以下のコードで 440Hz と 880Hz のコサイン信号を作成します。

>> sig1='cos440.ogg';                               %creating the audio file @440 Hz  
>> sig2='cos880.ogg';                               %creating the audio file @880 Hz  
>> fs=44100;                                             %generating the parameters values (Period, sampling frequency and angular frequency)  
>> t=0:1/fs:0.02;
>> w1=2*pi*440*t;
>> w2=2*pi*880*t;
>> audiowrite(sig1,cos(w1),fs);         %writing the function cos(w) on the files created  
>> audiowrite(sig2,cos(w2),fs);

ここで両信号をプロットしてみます。

信号1（440 Hz）のプロット

>> [y1, fs] = audioread(sig1);
>> plot(y1)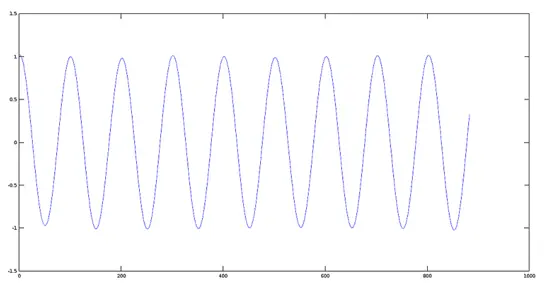

440Hzのコサイン信号の波形

信号2（880 Hz）のプロット

>> [y2, fs] = audioread(sig2);
>> plot(y2)

880Hzのコサイン信号の波形

手順 2: 2つの信号を加算する

前で作成した2つの信号を単純に足します。

>> sumres=y1+y2;
>> plot(sumres)

加算された信号の波形

加算すると、元の2つの成分が重なって聞こえ、音色が複雑になります。ギター用のエフェクト「オクターバー（Octaver）」はこの特性を利用し、音を上下のオクターブで重ねて同時に鳴らします。

手順 3: 実際の音源の加算（グレゴリオ聖歌の例）

ここではサンプルとして2つの声のトラックを読み込み、加算してミックス結果を確認します。

Avemariaトラックの読み込みとプロット

>> [y1,fs]=audioread('avemaria_.ogg');
>> plot(y1)

Avemariaの波形

Hymnusトラックの読み込みとプロット

>> [y2,fs]=audioread('hymnus.ogg');
>> plot(y2)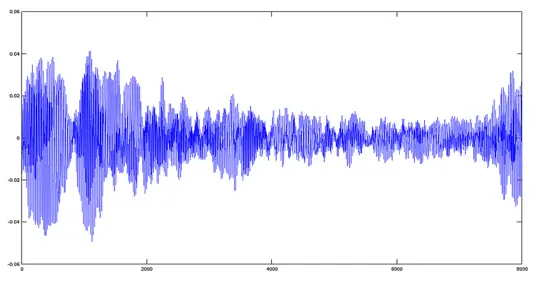

Hymnusの波形

Avemaria と Hymnus の加算

>> y='avehymnus.ogg';
>> audiowrite(y, y1+y2, fs);
>> [y, fs]=audioread('avehymnus.ogg');
>> plot(y)

AvemariaとHymnusを合成した波形

音声の観点では、両トラックがミックスされた音として聞こえます。位相差や振幅差により一部の周波数が強調または打ち消される点に注意してください。

信号の乗算

信号同士の乗算は、時間領域で値ごとに積を取る操作です。乗算によって変調（モジュレーション）や新たな周波数成分の生成が起こります。

R(t) = S1(t) * S2(t)

以下は先ほどの cos440 と cos880 を使った例です。

>> sig1='cos440.ogg';                               %creating the audio file @440 Hz  
>> sig2='cos880.ogg';                               %creating the audio file @880 Hz  
>> product='prod.ogg';                              %creating the audio file for product  
>> fs=44100;                                             %generating the parameters values (Period, sampling frequency and angular frequency)  
>> t=0:1/fs:0.02;
>> w1=2*pi*440*t;
>> w2=2*pi*880*t;
>> audiowrite(sig1, cos(w1), fs);       %writing the function cos(w) on the files created  
>> audiowrite(sig2, cos(w2), fs);
>> [y1,fs]=audioread(sig1);
>> [y2,fs]=audioread(sig2);
>> audiowrite(product, y1.*y2, fs); %performing the product
>> [yprod,fs]=audioread(product);
>> plot(yprod);                         %plotting the product

注: 値ごとの積を計算するために演算子 ‘.*’ を使う必要があります。これはベクトル（または行列）同士の要素ごとの積を表します。

乗算結果のプロット

乗算による波形

周波数が大きく異なる2信号の乗算（変調の原理）

ここでは搬送波と変調信号の例で、乗算がどのように見えるかを説明します。

ステップ 1: 220 Hz の搬送波を作る

>> fs=44100;
>> t=0:1/fs:0.03;
>> w=2*pi*220*t;
>> y1=cos(w);
>> plot(y1);

搬送波 220Hz の波形

ステップ 2: 高周波（変調）信号を作る（例: 22kHz）

>> y2=cos(100*w);
>> plot(y2);

変調信号の波形（高周波）

ステップ 3: 乗算してプロット

>> plot(y1.*y2);

変調された信号の波形

この乗算により、元の周波数の和と差（側帯波）が生じ、スペクトルが拡大・移動します。これは振幅変調（AM）の基本です。

信号をスカラー倍する

関数をスカラー K で掛ける操作は振幅を拡大・縮小し、Kが負なら位相反転を引き起こします。

R(t) = K * F(t)

以下は実例です。

>> [y,fs]=audioread('cos440.ogg');
>> res1='coslow.ogg';
>> res2='coshigh.ogg';
>> res3='cosinverted.ogg';
>> K1=0.2;
>> K2=0.5;
>> K3=-1;
>> audiowrite(res1, K1*y, fs);
>> audiowrite(res2, K2*y, fs);
>> audiowrite(res3, K3*y, fs);

元の信号のプロット

>> plot(y)

元のコサイン波形

振幅を0.2に縮小した信号のプロット

>> plot(res1)

振幅が0.2に縮小された波形

振幅を0.5に縮小した信号のプロット

>> plot(res2)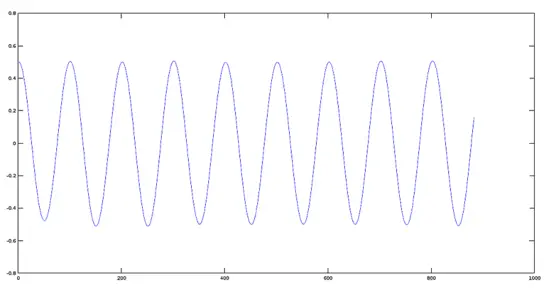

振幅が0.5に縮小された波形

位相が反転した信号のプロット

>> plot(res3)

位相が反転したコサイン波形

実践的な注意点

重要: 加算や乗算は簡単に行えますが、実運用ではサンプリング周波数の一致、信号長の一致（ゼロパディングの必要性）、クリッピングの回避、位相やレベル合わせに注意してください。特に加算時はピークが増幅し、クリップしてしまうと歪みが生じます。

付加価値セクション

ファクトボックス: キー数値

標本化周波数の例: 44100 Hz（CD規格）
コサインの例: 440 Hz（楽音A）と880 Hz（1オクターブ上）
乗算で生成される成分: 搬送波周波数の和と差（上側帯と下側帯）

ミニ手順書（Signal Add/Multiply チェックリスト）

すべてのトラックが同じ fs（サンプリング周波数）であることを確認する。
信号長が異なる場合はゼロパディングまたは切り詰めを行う。
加算する前に振幅レベルを正規化する（クリップ防止）。
乗算では ‘.*’ を使って要素ごとの積を取る。
結果をプロットして時間波形とスペクトルを確認する。

いつこの方法が適切でないか（反例）

同期されていない複数トラックを単純加算すると位相の打ち消しや位相干渉が発生し、意図しない音色変化や音量低下を引き起こす場合があります。
非線形処理やフィルタ処理が必要な場合（リバーブ、イコライザなど）は、単純加算や乗算だけでは期待する結果が得られないことがあります。

メンタルモデルとヒューリスティック

加算は「重ね合わせ」：複数の音源を同時に鳴らすイメージ。ピークレベルに注意。
乗算は「変調」：ある信号が別の信号の包絡や振幅を制御し、新しい周波数成分を作る。
スカラー倍は「音量調整と位相反転」：単純だが後の処理に大きく影響する。

役割別チェックリスト

録音エンジニア: サンプリング周波数とゲイン構成を保持し、クリップを避ける。
サウンドデザイナー: 乗算で意図的に新しい倍音を作り、フィルタで整形する。
研究者/学生: 結果のスペクトル解析（FFT）で副次成分を定量的に確認する。

一行用語集

加算: 時間領域で値を足す操作
乗算: 時間領域で値を掛ける操作（変調を生む）
スカラー倍: 振幅を拡大/縮小、負の値で位相反転

テストケースと受入基準

同じ波形長・同じfsの二つの正弦波を加算し、FFTで両周波数成分が現れること。
高周波の変調波と低周波の搬送波を乗算し、変調後に副次成分（和/差周波数）が確認できること。
スカラー K を掛けた結果の最大振幅が元の振幅に K を掛けた値に一致すること（クリップを除く）。

まとめ

基本的な代数演算（加算、乗算、スカラー倍）は音声信号処理の基礎です。これらの操作を理解することで、ミキシング、振幅変調、スペクトル操作など、より高度な技術へスムーズに進むことができます。次回はスペクトル解析や実際の変調実験を通じて、これらの操作が周波数領域でどのように見えるかを詳しく扱います。

重要: 実験では必ずレベル管理とサンプリング整合性をチェックしてください。過大な振幅はクリッピングを生み、結果が正しくなくなります。

信号の加算と乗算: Octaveでの音声信号操作