Signaloperationen in Octave: Addition, Multiplikation und Skalierung von Audiosignalen

Einführung

In der vorherigen Anleitung haben wir gezeigt, wie man Audiodateien liest, schreibt und abspielt sowie eine Audiodatei aus einer periodischen Funktion (z. B. Kosinus) synthetisiert. In diesem Tutorial demonstriere ich, wie man Signale addiert, Signale multipliziert (Modulation) und wie sich Skalierung (Multiplikation mit einem Skalar) auf ein Signal auswirkt. Diese grundlegenden Operationen sind die Grundlage für komplexere Techniken wie Spektralanalyse und Amplituden- oder Phasenmodulation.

Wichtig: Alle Codebeispiele verwenden Octave/Matlab-kompatible Befehle und setzen eine Abtastrate fs = 44100 Hz voraus.

Übersicht der Schlüsselbegriffe

• Signal: Eine zeitabhängige Folge von Werten, meist Audiodaten.
• Abtastrate (fs): Anzahl Abtastwerte pro Sekunde, hier 44100 Hz.
• Modulation: Multiplikation zweier Signale, dabei entstehen neue Frequenzanteile.

Addition von Signalen

Die Summe zweier Signale S1(t) und S2(t) ergibt ein Signal R(t), dessen Wert zu jedem Zeitpunkt die Summe der einzelnen Signalwerte ist:

R(t) = S1(t) + S2(t)

Wir erzeugen zwei Sinussignale unterschiedlicher Frequenz und addieren sie in Octave, um das Ergebnis grafisch zu untersuchen.

Schritt 1: Zwei Signale unterschiedlicher Frequenz erzeugen (ogg-Dateien)

>> sig1='cos440.ogg';                     % Erzeuge Audiodatei @440 Hz
>> sig2='cos880.ogg';                     % Erzeuge Audiodatei @880 Hz
>> fs=44100;                              % Abtastrate in Hz
>> t=0:1/fs:0.02;
>> w1=2*pi*440*t;
>> w2=2*pi*880*t;
>> audiowrite(sig1,cos(w1),fs);           % Schreibe cos(w1) in Datei
>> audiowrite(sig2,cos(w2),fs);

Nun plotten wir beide Signale getrennt.

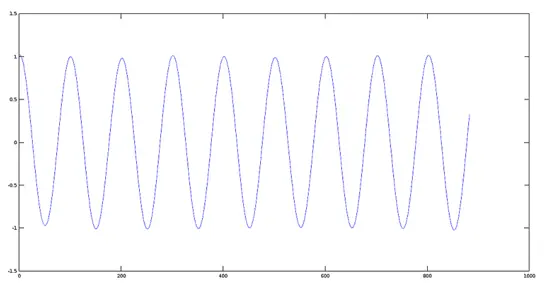
Plot von Signal 1 (440 Hz)

>> [y1, fs] = audioread(sig1);
>> plot(y1)

Plot von Signal 2 (880 Hz)

>> [y2, fs] = audioread(sig2);
>> plot(y2)

Schritt 2: Addition der beiden Signale

Jetzt führen wir die Summe der zuvor erzeugten Signale aus:

>> sumres=y1+y2;
>> plot(sumres)

Hinweis: Wenn die Signale unterschiedlich gepolt oder unterschiedlich skaliert sind, kann die Addition zu Übersteuerung (Clipping) führen. Achten Sie ggf. auf Normierung.

Wichtig: Der “Octaver”-Effekt entsteht, wenn man das Signal so kombiniert, dass eine Kopie des Originals in einer höheren oder tieferen Oktave gleichzeitig erklingt. Das Ergebnis kann musikalisch nützlich sein, weil zwei identisch klingende Töne in unterschiedlichen Oktaven auftreten.

Schritt 3: Addition realer Audiospuren (Beispiel: zwei gregorianische Gesänge)

Als praktisches Beispiel mischen wir zwei Sprach-/Choraufnahmen.

Avemaria-Track

>> [y1,fs]=audioread('avemaria_.ogg');
>> plot(y1)

Hymnus-Track

>> [y2,fs]=audioread('hymnus.ogg');
>> plot(y2)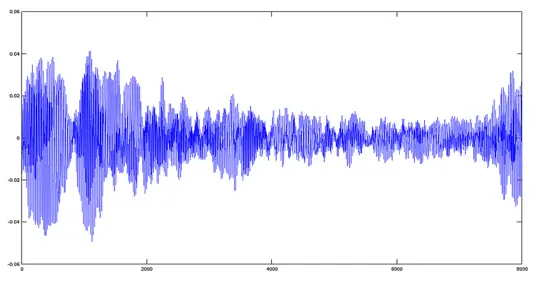

Avemaria + Hymnus (Summenmischung)

>> y='avehymnus.ogg';
>> audiowrite(y, y1+y2, fs);
>> [y, fs]=audioread('avehymnus.ogg');
>> plot(y)

Klanglich ergibt die Addition eine Mischung beider Tracks. Dies ist das einfachste Mischverfahren; in Produktionsworkflows folgen typischerweise Pegelanpassung, EQ und Dynamikbearbeitung.

Produkt (Multiplikation) von zwei Signalen

Die Multiplikation zweier Signale erfolgt elementweise und führt, je nach Frequenzrelation der Signale, zu Interferenz und zur Entstehung neuer Frequenzkomponenten (Summe und Differenz der Grundfrequenzen). Mathematisch:

R(t) = S1(t) * S2(t)

Beispiel mit vorher erzeugten Dateien:

>> sig1='cos440.ogg';                     % Erzeuge Audiodatei @440 Hz
>> sig2='cos880.ogg';                     % Erzeuge Audiodatei @880 Hz
>> product='prod.ogg';                    % Ausgabedatei für Produkt
>> fs=44100;
>> t=0:1/fs:0.02;
>> w1=2*pi*440*t;
>> w2=2*pi*880*t;
>> audiowrite(sig1, cos(w1), fs);
>> audiowrite(sig2, cos(w2), fs);
>> [y1,fs]=audioread(sig1);
>> [y2,fs]=audioread(sig2);
>> audiowrite(product, y1.*y2, fs);      % Elementweise Multiplikation
>> [yprod,fs]=audioread(product);
>> plot(yprod);

Hinweis: Verwenden Sie den Operator ‘.*’ für elementweise Operationen in Octave/Matlab.

Plot des Produkt-Signals

Graphischer Effekt bei großer Grundfrequenzdifferenz (Prinzip der Modulation)

Wenn ein niedrigfrequentes Signal (Träger) mit einem deutlich höherfrequenten Signal (Modulator) multipliziert wird, entstehen Amplitudenhüllungen und neue Frequenzkomponenten. Beispiel:

Schritt 1: Trägersignal 220 Hz

>> fs=44100;
>> t=0:1/fs:0.03;
>> w=2*pi*220*t;
>> y1=cos(w);
>> plot(y1);

Schritt 2: Höheres moduliertes Signal (hier als Vielfaches)

>> y2=cos(100*w);
>> plot(y2);

Schritt 3: Multiplikation (Moduliertes Signal)

>> plot(y1.*y2);

Akustisch erzeugt die Multiplikation Oberwellen und Seitenbänder (Amplitudenmodulation). In Anwendungen wie AM-Radio oder Effekten ist genau dieses Verhalten erwünscht.

Multiplikation eines Signals mit einem Skalar

Die Multiplikation eines Signals F(t) mit einem Skalar K ändert die Amplitude und ggf. die Phase (bei negativem K). Definition:

R(t) = K * F(t)

Beispiel:

>> [y,fs]=audioread('cos440.ogg');         % Arbeitsdatei
>> res1='coslow.ogg';
>> res2='coshigh.ogg';
>> res3='cosinverted.ogg';
>> K1=0.2;                                  % Skalarwerte
>> K2=0.5;
>> K3=-1;
>> audiowrite(res1, K1*y, fs);              % Signal skaliert um 0.2
>> audiowrite(res2, K2*y, fs);
>> audiowrite(res3, K3*y, fs);              % invertiertes Signal

Plot des Originalsignals

>> plot(y)

Plot: Signal mit Amplitudenreduktion 0.2

>> plot(res1)

Plot: Signal mit Amplitudenreduktion 0.5

>> plot(res2)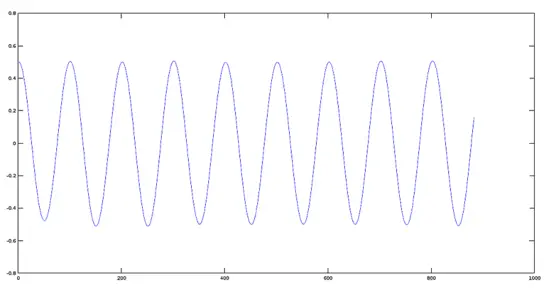

Plot: Signal mit invertierter Phase

>> plot(res3)

Skalierung ist die einfachste Form der Lautstärkeregelung. Negative Skalare drehen das Signal um 180° (Phaseninvertierung).

Praktische Hinweise, Fehlerfälle und Alternativen

Wichtig: Bei allen Operationen sollten die Signallängen/Abtastraten übereinstimmen. Falls nicht, führen Sie Resampling oder Padding durch, sonst entstehen Laufzeitfehler oder unerwartete Ergebnisse.

Wann es fehlschlägt

• Unterschiedliche fs-Werte: Audioread mit unterschiedlichen Abtastraten erfordert Resampling.
• Unterschiedliche Kanäle (Mono vs. Stereo): Achten Sie auf Dimensionen; ggf. auf Mono mixen oder beide Kanäle getrennt verarbeiten.
• Clipping: Summen können Werte > ±1 erzeugen; normalisieren oder Limiter verwenden.

Alternative Ansätze

• Für Mixe in der Musikproduktion: Verwenden Sie Gain-Staging, Equalizer und Limiter statt reiner Addition.
• Für Modulationen: Verwenden Sie Bibliotheken für AM/FM, die Fensterung und Anti-Alias-Filter bieten.

Mentaler Modellansatz

• Addition: Überlagerung von Formen—Amplitude addiert sich punktweise.
• Multiplikation: Amplitudenhüllung und Spektralerweiterung—denke in Seitenbändern.
• Skalierung: Lautstärke und PolaritÄt ändernd.

Kurze Methodik (Mini-Checklist zum Arbeiten in Octave)

1. Prüfen Sie fs aller Dateien: [y, fs] = audioread(…)
2. Vereinheitlichen Sie Kanalanzahl (mono/stereo).
3. Normalisieren, falls notwendig: y = y / max(abs(y));
4. Führen Sie Operation aus ( + , . , K )
5. Prüfen Sie Ergebnis visuell und auditiv; vermeiden Sie Clipping.

Rollenbasierte Checkliste

• Entwickler: Automatisieren Sie Resampling und Prüfungen in Skripten.
• Audio-Engineer: Verwenden Sie Gain-Staging und Metering vor Summen.
• Forscher: Analysieren Sie Spektren vor und nach Operationen (FFT).

Einfache Testfälle / Akzeptanzkriterien

• Wenn y1 und y2 identisch sind, dann y1+y2 = 2*y1 (skalar multipliziert).
• Multiplikation zweier Monofiles mit identischer Frequenz: Ergebnis sollte sichtbar moduliert erscheinen.
• Skalierung mit K=-1 muss genau die Inversion des Signals erzeugen.

Fazit

Algebraische Summe, elementweise Produktbildung und Multiplikation mit Skalaren sind grundlegende Werkzeuge der digitalen Signalverarbeitung. Sie bilden die Basis für komplexere Prozesse wie Spektralanalyse und verschiedene Arten der Modulation. In der nächsten Anleitung behandeln wir Spektralanalyse und die Anwendung dieser Operationen im Frequenzraum.

Zusammenfassung:

• Prüfung von Abtastrate und Kanälen ist Pflicht vor Operationen.
• Verwenden Sie elementweise Operatoren (.*) für Produkte.
• Normierung schützt vor Clipping nach Addition.

Wichtig: Testen Sie Änderungen immer sowohl visuell (Plot) als auch auditiv (Anhören), um unerwünschte Artefakte rechtzeitig zu erkennen.