Octave에서 오디오 신호 연산: 합과 곱

중요: 두 오디오 파일을 합하거나 곱하려면 샘플레이트(fs)와 배열 길이(샘플 수)가 동일해야 합니다. 다르다면 리샘플링(resample) 또는 잘라내기/패딩 작업이 필요합니다.

개요

이전 튜토리얼에서는 오디오 파일을 읽고 쓰고 재생하는 방법과 주기함수(예: 코사인)로 오디오 파일을 합성하는 법을 보았습니다. 이번 글에서는 신호의 합(addition), 곱(product, 즉 변조의 기초)과 스칼라 곱(scalar multiplication)이 원본 신호에 미치는 효과를 실습과 그래프로 확인합니다. 실습은 Octave(또는 MATLAB 호환 환경)를 기반으로 합니다.

용어 한 줄 정의:

• 샘플레이트(fs): 초당 샘플 수, 여기서는 44100 Hz를 사용합니다.

신호 더하기

두 신호 S1(t)과 S2(t)의 합 R(t)는 임의의 시점에서 두 신호 값의 합입니다:

R(t) = S1(t) + S2(t)

다음 예제에서는 서로 다른 주파수의 코사인 신호 두 개를 만들고 합한 결과를 그래프로 확인합니다.

단계 1: 서로 다른 주파수의 두 신호 만들기 (ogg 파일)

>> sig1='cos440.ogg';                   %creating the audio file @440 Hz  
>> sig2='cos880.ogg';                   %creating the audio file @880 Hz  
>> fs=44100;                            %generating the parameters values (Period, sampling frequency and angular frequency)  
>> t=0:1/fs:0.02;  
>> w1=2*pi*440*t;  
>> w2=2*pi*880*t;  
>> audiowrite(sig1,cos(w1),fs);     %writing the function cos(w) on the files created  
>> audiowrite(sig2,cos(w2),fs);

다음은 각각을 읽어 플롯한 코드입니다.

>> [y1, fs] = audioread(sig1);  
>> plot(y1)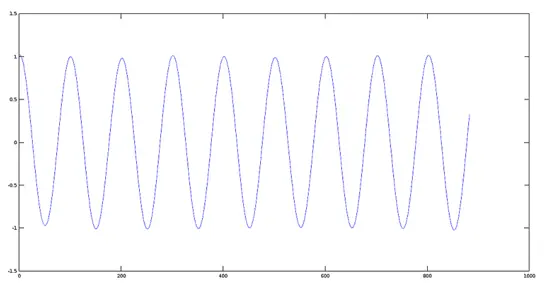

>> [y2, fs] = audioread(sig2);  
>> plot(y2)

단계 2: 두 신호 더하기

>> sumres=y1+y2;  
>> plot(sumres)

설명: 위 예에서는 두 주파수가 서로 겹쳐 보이지만 실제로는 두 개의 성분(440Hz와 880Hz)이 합성되어 합성파형을 만듭니다. 음향적으로는 두 음이 동시에 들리며 위상이나 진폭에 따라 간섭(보강/상쇄)이 발생할 수 있습니다.

옥베이터(Octaver) 효과 설명

옥베이터는 연주된 음을 낮거나 높이는(옥타브 변경) 기능을 제공합니다. 원래 음과 변환된 음을 함께 들려주면 두 음이 동시에 들리며 특유의 풍부한 소리가 납니다. 이 튜토리얼의 신호 합성은 옥베이터 원리를 단순히 시뮬레이션하는 기초가 됩니다.

단계 3: 실제 트랙 두 개 더하기 (그레고리안 성가 예)

아래 예제는 두 개의 보컬 샘플을 더해 믹스하는 방법을 보여줍니다.

>> [y1,fs]=audioread('avemaria_.ogg');  
>> plot(y1)

>> [y2,fs]=audioread('hymnus.ogg');  
>> plot(y2)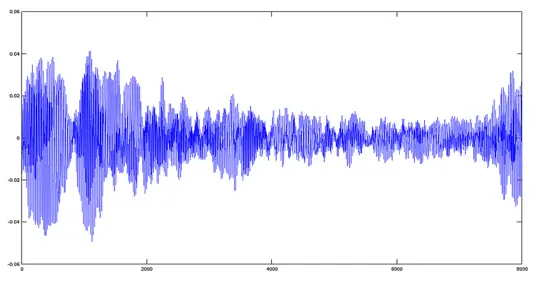

>> y='avehymnus.ogg';  
>> audiowrite(y, y1+y2, fs);  
>> [y, fs]=audioread('avehymnus.ogg');  
>> plot(y)

오디오 관점에서 결과는 두 트랙이 혼합되어 동시에 들립니다. 실제 믹싱에서는 레벨(게인) 조정, 팬닝, EQ, 리샘플링 등 추가 처리가 필요합니다.

노트: 두 신호를 단순히 더할 때 합이 -1..1 범위를 벗어나면 클리핑이 발생합니다. 필요한 경우 정규화(normalize)하거나 페이더 게인을 적용하세요.

신호의 곱 (Product)

두 신호의 곱은 요소별 곱셈을 의미합니다: R(t) = S1(t) * S2(t). 곱셈은 변조(modulation)의 기초입니다. 다음은 같은 예제로 곱셈을 수행하는 코드입니다.

>> sig1='cos440.ogg';                   %creating the audio file @440 Hz  
>> sig2='cos880.ogg';                   %creating the audio file @880 Hz  
>> product='prod.ogg';              %creating the audio file for product  
>> fs=44100;                            %generating the parameters values (Period, sampling frequency and angular frequency)  
>> t=0:1/fs:0.02;  
>> w1=2*pi*440*t;  
>> w2=2*pi*880*t;  
>> audiowrite(sig1, cos(w1), fs);       %writing the function cos(w) on the files created  
>> audiowrite(sig2, cos(w2), fs);  
>> [y1,fs]=audioread(sig1);  
>> [y2,fs]=audioread(sig2);  
>> audiowrite(product, y1.*y2, fs);    %performing the product  
>> [yprod,fs]=audioread(product);  
>> plot(yprod);                 %plotting the product

중요: 요소별 곱셈을 위해 반드시 ‘.‘ 연산자를 사용하세요. 일반 행렬 곱셈 ‘‘은 의도한 시간샘플별 연산을 수행하지 않습니다.

곱셈 결과 플롯

큰 기본 주파수 차이를 가진 신호 곱셈 — 변조의 원리

다음 실습은 캐리어(carrier) 신호와 높은 주파수의 변조 신호를 곱했을 때의 파형 변화를 보여줍니다. 이는 진폭변조(AM)나 곱셈 기반 변조의 기초를 이해하는 데 유용합니다.

Step 1: 220Hz 캐리어 생성

>> fs=44100;  
>> t=0:1/fs:0.03;  
>> w=2*pi*220*t;  
>> y1=cos(w);  
>> plot(y1);

Step 2: 변조용 고주파(22000Hz 근사) 생성

>> y2=cos(100*w);  
>> plot(y2);

Step 3: 곱셈(변조) 및 플롯

>> plot(y1.*y2);

해석: 곱셈은 주파수 성분을 섞어 사이드밴드(sidebands)를 생성합니다. 원리적으로 두 사인파의 곱은 합주파수와 차주파수를 포함하는 성분을 만듭니다.

신호를 스칼라로 곱하기

신호에 스칼라 K를 곱하면 진폭이 변경되고, 음의 스칼라를 사용하면 위상이 반전됩니다. 수식으로는 R(t) = K * F(t)입니다.

>> [y,fs]=audioread('cos440.ogg');      %creating the work files  
>> res1='coslow.ogg';                  
>> res2='coshigh.ogg';  
>> res3='cosinverted.ogg';  
>> K1=0.2;                          %values of the scalars  
>> K2=0.5;  
>> K3=-1;  
>> audiowrite(res1, K1*y, fs);          %product function-scalar  
>> audiowrite(res2, K2*y, fs);  
>> audiowrite(res3, K3*y, fs);

>> plot(y)

>> plot(res1)

>> plot(res2)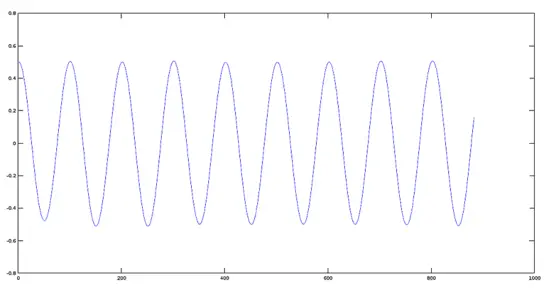

>> plot(res3)

설명: 스칼라 곱은 게인 조정(gain control)과 동등합니다. 믹싱 전 레벨 조정이나 페이더 구현에 사용됩니다.

추가 관점: 언제 작동하지 않는가 / 주의사항

• 샘플레이트 불일치: 파일들이 다른 fs를 가지면 단순 덧셈/곱셈으로 왜곡됩니다. 반드시 리샘플링하세요.
• 길이 불일치: 두 배열의 길이가 다르면 오류가 발생하거나 의도치 않은 패딩이 필요합니다.
• 클리핑: 합 연산 결과가 범위를 초과하면 디스토션이 생깁니다. 정규화 또는 리미팅을 적용하세요.
• 스테레오/모노 불일치: 채널 수가 다르면 채널 매핑이 필요합니다.

대안 및 확장

• 믹싱(합): 단순 합 대신 RMS 기반 정규화, LUFS 기준 라우팅, 또는 페이더-감쇠(gain staging)를 사용해 음량을 제어하세요.
• 변조(곱): AM/DSB-SC/SSB 같은 표준 변조 기법을 적용하면 더 통제된 스펙트럼을 얻습니다.
• 필터링: 곱셈 후 저역/고역 필터를 적용해 불필요한 사이드밴드를 제거하세요.

빠른 핵심 수치(팩트박스)

• 샘플레이트(fs) 예시: 44100 Hz
• 예제 지속시간: 0.02 s, 0.03 s
• 사용 주파수 예: 220 Hz, 440 Hz, 880 Hz, (변조에서 22000 Hz 근사)
• 요소별 곱셈 연산자: ‘.*’

검사 목록(엔지니어/뮤지션용)

• 엔지니어:

  • 모든 파일이 동일한 fs인가?
  • 배열 길이가 맞는가(또는 적절히 패딩/트리밍되었는가)?
  • 결과가 클리핑되지 않았는가(최대값 확인)?

• 뮤지션/제작자:

  • 각 트랙의 게인을 미리 설정했는가?
  • 원하지 않는 위상 반전이 없는가?
  • 스테레오 이미징(팬닝)은 의도한 대로인가?

간단한 테스트 케이스 / 수락 기준

• 입력: 동일한 길이와 fs를 가진 cos440.ogg와 cos880.ogg
• 작업: y = y1 + y2
• 기대 결과: 재생 시 두 주파수 성분(440Hz, 880Hz)이 동시에 들려야 함. 파형은 두 성분의 합으로 보임.
• 실패 판단: 재생에서 잡음, 클리핑, 또는 한 성분만 들리면 실패.

1줄 용어집

• 합성(summation): 시간 도메인에서 샘플 값을 더하는 연산.
• 곱셈(product): 시간 도메인에서 샘플 값을 요소별 곱하는 연산. 변조를 만듦.
• 스칼라 곱: 전체 신호를 일정 비율(K)로 곱해 진폭을 조정.

워크플로(간단 SOP)

1. 모든 소스 파일을 읽고(fs, 채널, 길이 확인).
2. 필요하면 리샘플링 또는 트리밍/패딩 수행.
3. 연산(합/곱/스칼라 곱) 수행.
4. 결과 확인: 최대값·RMS·음색 검사, 필요한 경우 정규화/리미트.
5. 파일로 저장하고 재생 확인.

결론

기본 수학 연산(덧셈, 곱셈, 스칼라 곱)은 스펙트럼 분석, 진폭 변조(AM), 위상/주파수 변조 같은 고급 오디오 처리의 기초입니다. 이 튜토리얼에서 본 예제는 Octave에서 이런 연산을 직접 수행하고 결과를 시각적으로 확인하는 방법을 보여줍니다. 다음 튜토리얼에서는 이러한 연산을 응용한 스펙트럼 분석과 다양한 변조 기법의 청각 및 스펙트럼 효과를 살펴보겠습니다.

요약:

• 덧셈: 신호 합성(믹싱), 샘플 수·샘플레이트 일치 필요
• 곱셈: 변조의 기초, 요소별 연산 ‘.*’ 사용
• 스칼라 곱: 진폭 조정 및 위상 반전 가능