目次
- 変調とは
- 振幅変調
- なぜ振幅変調を使うのか
- トレモロ効果
- 実際の音声ファイルへ適用する手順
- 周波数変化(周波数変調の例)
- 実践ミニ手順(方法論)
- 役割別チェックリスト
- テストケースと受入基準
- 用語集
- まとめと重要ポイント
変調
変調とは、ある信号(メッセージ)を別の信号(搬送波)に埋め込む操作です。音声処理では、信号の振幅や周波数を時間的に変化させて新しい音響効果を作ります。1行定義: 搬送波は情報を運ぶ正弦波や周期波です。
振幅変調
その名前が示す通り、振幅変調は搬送波の振幅を伝えたいメッセージ信号で変化させます。搬送波(キャリア)は情報を「運ぶ」役割を持ちます。振幅変調は商業放送や市民バンドの送信(AM)などに利用されます。
なぜ振幅変調を使うのか
重要: 下記の理由は電波伝搬や機器設計の観点を含みますが、音響用途では主に「エフェクト生成」の容易さのために使います。
放射のための周波数シフト
自由空間の通信では、送受信用に効率的な電磁放射アンテナが必要です。アンテナ長は放射する波長と同程度の大きさが望ましいため、音声成分のように周波数が非常に低い信号(例: 100 Hz以下)を直接放射すると、現実的でない長さのアンテナが必要になります。信号を高周波の搬送波(例: 100 MHz)に印刷すれば、アンテナ長は数メートル程度で済みます。
多重化と周波数分配
1つの通信チャネルを複数の信号が共有する場合、異なる信号を異なる周波数帯に移すことで受信側が選択できます。これはテレメトリ、FMステレオ、多地点通信などで使われます。
機器設計上の制約回避
フィルタや増幅器の設計は、信号の周波数位置によって大きく容易さが変わります。モジュレーションにより信号を扱いやすい周波数帯に移動したり、広帯域信号を準狭帯域に見せかけることで機器設計を簡素化できます。
音響エフェクトとしての利用
音響分野では、振幅変調は特に扱いやすいため、トレモロ、コーラス、フランジャーなど多くのエフェクトで使われます。本チュートリアルはこの用途に焦点を当てます。
トレモロ効果
トレモロは振幅変調の最もシンプルな応用の一つです。音声信号を周期的な波(正弦波など)で乗算することで実現します。以下は基本的な実装例です。
>> tremolo='tremolo.ogg';
>> fs=44100;
>> t=0:1/fs:10;
>> wo=2*pi*440*t;
>> wa=2*pi*1.2*t;
>> audiowrite(tremolo, cos(wa).*cos(wo),fs);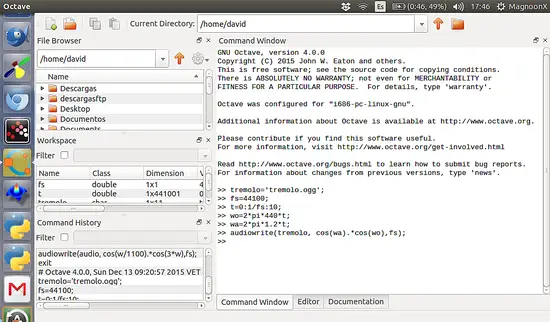
上記は正弦波の振幅が周期的に変化する信号を生成します。聴感上は「トレモロ」に相当します。
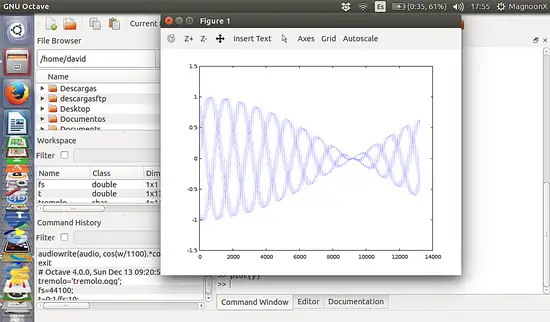
実際の音声ファイルへのトレモロ適用手順
以下は録音済みの男性の声(発音: ‘A’)にトレモロを適用する例です。元信号のプロットと包絡生成、乗算、書き出しまでを示します。
>> [y,fs]=audioread('A.ogg');
>> plot(y);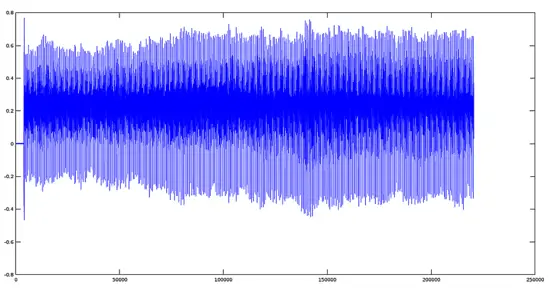
包絡(エンベロープ)は次のパラメータで作成します。
- 振幅 = 1
- 周波数 = 1.5 Hz
- 位相 = 0
>> t=0:1/fs:4.99999999;
>> t=t(:);
>> w=2*pi*1.5*t;
>> q=cos(w);
>> plot(q);Note: 時間配列はデフォルトで列ベクトルで生成されることがあります。信号との要素ごとの乗算を正しく行うために、形状を合わせる(ここでは明示的な縦ベクトル化 t=t(:) を使う)必要があります。
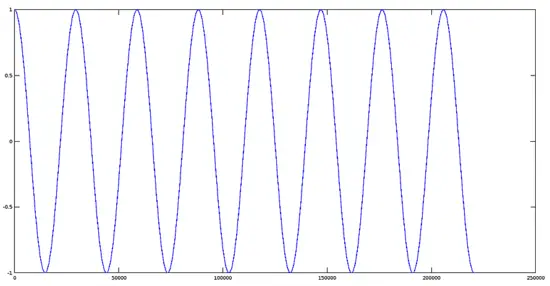
乗算してファイルを作成します。
>> tremolo='tremolo.ogg';
>> audiowrite(tremolo, q.*y,fs);
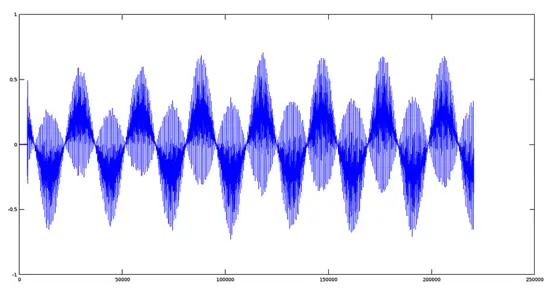
重要: 包絡信号 q の振幅レンジは元の信号 y に対してクリッピングやDCシフトを引き起こす場合があります。必要に応じて q を正規化したりオフセット(例: 0.5 + 0.5*cos(w))を追加して負の振幅を避けると安全です。
周波数変化
周波数を時間的に変化させることで、ディストーションや映画・ゲームのサウンドエフェクトなど興味深い音響効果を得られます。以下に正弦波による単純な周波数変調の例を示します。
正弦による周波数変調の例
式の例(直感的表現):
Y = Ac cos( wo cos(wo/k) )
ここで:
- Ac = 振幅
- wo = 基本角周波数
- k = スカラー除数
実装例:
>> fm='fm.ogg';
>> fs=44100;
>> t=0:1/fs:10;
>> w=2*pi*442*t;
>> audiowrite(fm, cos(cos(w/1500).*w), fs);
>> [y,fs]=audioread('fm.ogg');
>> figure (); plot (y);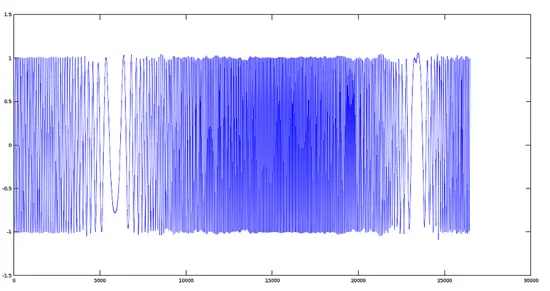
ほとんど任意の周期関数を周波数変調器として使えます。本例では正弦波を使いましたが、矩形波やノイズ、非正弦波を組み合わせると別の音響テクスチャが得られます。周波数比や変調深度を変えることで、鳴り方は大きく変化します。実験を推奨します。
実践ミニ手順(トレモロを適用する簡単な方法)
- 元音声ファイルを読み込む(サンプルレート fs を確認)
- 希望のトレモロ周波数 f_t(例 1〜8 Hz)と振幅レンジを決める
- 時間配列 t を作り、縦ベクトルに整形する
- 包絡 q(t) を生成する(例: 0.5 + 0.5*cos(2π f_t t) で全て正)
- q(t) と元信号 y を要素ごとに乗算する
- 結果を正規化してクリッピングを防ぐ
- オーディオファイルに書き出す
この順序はシンプルで再現性が高いので、まずここから試してください。
役割別チェックリスト
サウンドデザイナー
- トレモロ周波数のレンジ(低: 1–5Hz、中: 5–8Hz、高: >8Hz)を確認
- 包絡の形状(正弦、矩形、三角)を試す
- 出力をステレオでパンやディレイと組み合わせて試行
オーディオエンジニア
- 乗算前後のピークレベルを測定してクリッピングを防ぐ
- 必要ならリミッター/コンプレッサーを挿入
- サンプルレートと型(モノ/ステレオ)を維持
ソフトウェア開発者
- 数値配列の形状(行/列)を正しく扱う
- 処理をバッファ単位で行う場合は位相の継続性を保つ
- 異常入力(NaN、無音)へのガードを実装
テストケースと受入基準
基本機能テスト
- 入力: 単純正弦波 (440 Hz)。トレモロ f=2 Hz を適用。出力の包絡が2 Hzで変動していること。目視プロットで確認。
境界ケース
- f_t → 0.0 Hz のとき、包絡は定数となり出力は元信号のスケール変化のみであること。
- 高い f_t(例 > fs/2)では折り返しや意図しない変形が発生するため防ぐこと。
受入基準
- 出力波形にクリッピングがないこと(ピーク < -0.1 dBFS を推奨)
- 指定したトレモロ周波数で包絡が観測可能であること
典型的な失敗ケースと回避策
包絡信号の振幅が負になる場合
- 負振幅で乗算すると位相反転など望ましくない変化が起きる。オフセット(0.5 + 0.5*cos)で正に保つ。
時間配列の形状不一致
- 行列次元が合わない場合、要素ごとの乗算でエラーになる。縦ベクトル化やブロードキャストを確認。
サンプリング周波数のミスマッチ
- 包絡生成に使う fs と音声ファイルの fs が異なると時間ずれが生じる。常に fs を一元管理。
シンプルなチートシート(パラメータ例)
- トレモロ周波数: 0.5–8 Hz(ボーカルには 1–5 Hz が自然)
- 包絡オフセット: 0.5 + 0.5*cos(2π f t)(負値を避ける)
- 深さ(Depth): 0(オフ)–1(フル)で乗算前に線形補間
- 正規化: 出力 = 出力 / max(abs(output)) * 0.99
用語集(1行定義)
- 振幅変調: 搬送波の振幅をメッセージで変化させる操作
- 包絡: 信号の振幅を決定する時間的なスケール因子
- トレモロ: 振幅変調による周期的振れを利用した音響効果
- 周波数変調: 搬送波の周波数を時間的に変化させる操作
互換性とローカル注意点
- 多くのDAWやオーディオライブラリは同様の基本演算(乗算、正弦生成)を提供します。API 呼び出しやバッファ処理の詳細は環境に依存するため、サンプルレートとチャンネル数の整合性を常に確認してください。
まとめと重要ポイント
- 振幅変調は伝送だけでなく音響エフェクト生成でも有用です。トレモロはその最も基本的な応用です。
- 実装時は包絡の振幅レンジ、時間配列の形状、サンプリング周波数の整合性に注意してください。
- 周波数変調は豊かな音響バリエーションを生むので、関数形や深度を実験して好みのサウンドを作ってください。
重要: 実験の際はまず無音や単純波形で動作検証を行い、最終出力を正規化してクリッピングを回避してください。