Test statistici in Python: guida pratica

I test statistici verificano se differenze o associazioni nei dati sono dovute al caso o rappresentano effetti reali. In Python si usano librerie come Pingouin, SciPy, pandas e Seaborn per calcolare p-value, t-value, F-value e statistiche non parametriche. Pianifica ipotesi, alpha e dimensione del campione prima dell’analisi; usa test non parametrici quando i dati non soddisfano assunzioni.

Link rapidi

Che cos’è il test delle ipotesi?
Perché eseguire test statistici?
Test t di Student
Regressione lineare
ANOVA
Test non parametrici
Quando i test falliscono
Mini-metodologia passo-passo
Playbook e checklist

Logo di Python/Seaborn sovrapposto a un grafico stilizzato con barre, una linea ondulata e punti scatter, che rappresentano la visualizzazione dei dati.

Aggiornamento importante

Una versione precedente di questo articolo aveva invertito le definizioni di falsi positivi e falsi negativi. Un errore di Tipo I è un falso positivo, e un errore di Tipo II è un falso negativo. L’errore è stato corretto.

Aggiornamento: 27/09/2025 10:54 EST di David Delony

In test di ipotesi si possono commettere due errori principali: un errore di Tipo I (falso positivo), che si verifica quando si rifiuta l’ipotesi nulla mentre dovrebbe essere accettata; e un errore di Tipo II (falso negativo), che si verifica quando si accetta l’ipotesi nulla mentre dovrebbe essere rifiutata. Una difesa pratica contro entrambi è aumentare la dimensione del campione. Determina l’ipotesi nulla, l’alternativa e il livello di significatività prima di eseguire i test per evitare influenze post-hoc.

Che cos’è il test delle ipotesi?

Il test delle ipotesi è un insieme di tecniche statistiche che consentono di valutare se i risultati osservati in un campione sono compatibili con il caso o indicano un effetto reale. L’approccio standard prevede:

Formulare l’ipotesi nulla (H0): di solito afferma che non c’è effetto o nessuna differenza.
Formulare l’ipotesi alternativa (H1): afferma che esiste un effetto o una differenza.
Scegliere un livello di significatività alpha (es. 0,05 o 0,01).
Calcolare una statistica di test e il p-value.
Confrontare il p-value con alpha per decidere se rifiutare H0.

Definizione rapida: p-value è la probabilità, sotto l’ipotesi nulla, di osservare un risultato uguale o più estremo rispetto a quello ottenuto.

Nota importante

Un p-value piccolo non misura la grandezza dell’effetto: indica solo che l’effetto è improbabile sotto H0.
Effetto pratico e significatività statistica sono concetti distinti; valuta sempre la dimensione dell’effetto e gli intervalli di confidenza.

Perché eseguire test statistici?

I test statistici servono a distinguere segnali reali dal rumore. Esempi d’uso tipici:

Trial clinici: verificare se un farmaco modifica la pressione sanguigna.
Ricerca di mercato: confrontare tassi di conversione tra due versioni di una pagina.
Analisi di prodotto: capire se un cambiamento al prodotto migliora metriche chiave.

I test richiedono anche pensiero critico: definire ipotesi, pre-registrare il piano analitico quando possibile, considerare bias e confondenti.

Test t di Student

Il t-test confronta medie e funziona bene quando i dati sono approssimativamente normali e le varianze sono gestibili. Nella pratica, il t-test è spesso preferito al test z perché non richiede la deviazione standard della popolazione.

Tipi comuni di t-test:

Campione singolo: verifica se la media del campione è uguale a un valore noto.
Campioni indipendenti: confronta le medie di due gruppi diversi.
Campioni appaiati: confronta le medie prima/dopo sullo stesso soggetto.

Esempio pratico con Python e Pingouin

Importa NumPy e un generatore di numeri casuali:

import numpy as np
rng = np.random.default_rng()

Genera un campione di 15 valori distribuiti normalmente:

a = rng.standard_normal(15)

Verifica la normalità (Shapiro-Wilk) con Pingouin:

import pingouin as pg
pg.normality(a)

Risultato del test di normalità su un array usando Pingouin.

Esegui un t-test confrontando la media campionaria con 0.45:

pg.ttest(a, .45)

Interpretazione: se il p-value è alto (es. 0.99), non puoi rifiutare H0; i dati non forniscono evidenza contro l’ipotesi nulla a livelli di confidenza standard.

Quando usare il t-test

Campioni di dimensione moderata o grande con distribuzione approssimativamente normale.
Se la normalità è dubbia e il campione è piccolo, considera test non parametrici.

Regressione lineare

La regressione lineare valuta relazioni tra una variabile dipendente e una o più variabili indipendenti. Anche qui la statistica del test (t-value) e il p-value misurano se un coefficiente è significativamente diverso da zero.

Esempio con Seaborn e Pingouin

Seaborn fornisce dataset campione. Usiamo il dataset “tips” (mance) per esplorare la relazione tra conto totale e mancia.

import seaborn as sns
tips = sns.load_dataset('tips')

Mostriamo le prime righe del DataFrame (pandas) per capire le colonne disponibili:

tips.head()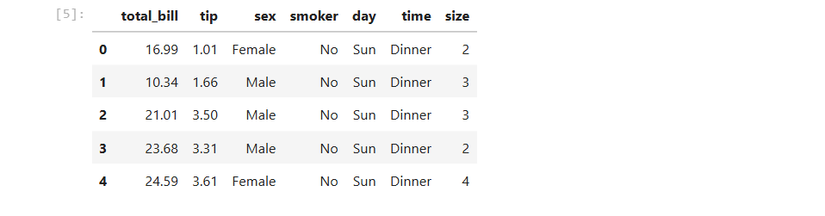

Tabella che mostra l'output di tips.head() in un notebook Jupyter.

Tracciamo un grafico scatter con la retta di regressione usando Seaborn:

sns.regplot(x='total_bill', y='tip', data=tips)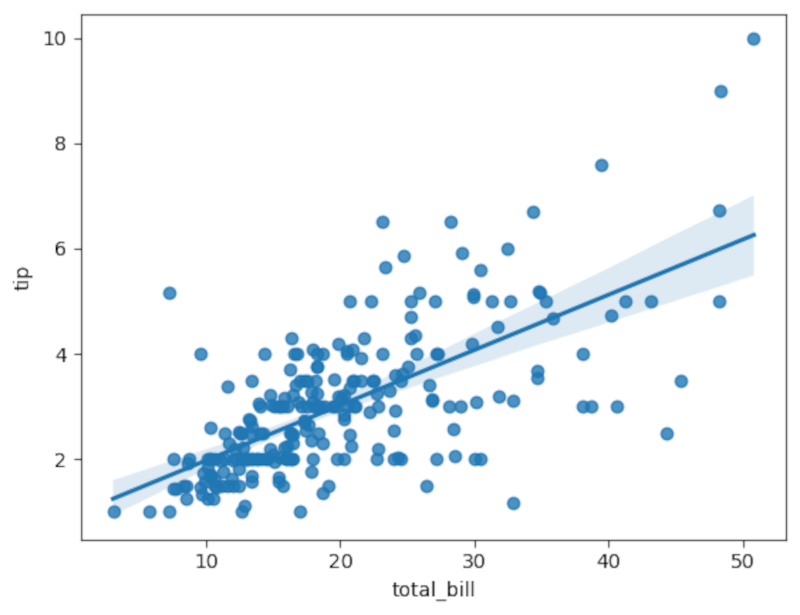

Regressione lineare di tip vs total_bill realizzata con Seaborn.

Per un’analisi formale con Pingouin:

pg.linear_regression(tips['tip'], tips['total_bill']).round(2)

Interpretazione: il test controlla l’ipotesi nulla che il coefficiente della pendenza sia 0. Un t-value grande e un p-value vicino a 0 indicano che la pendenza è significativamente diversa da zero.

Consiglio pratico

Guarda sempre anche l’intervallo di confidenza per capire l’incertezza della stima del coefficiente.
Valuta R-squared per la bontà di adattamento, ma ricorda che R-squared non prova causalità.

ANOVA

ANOVA (Analysis of Variance) confronta le medie di tre o più gruppi per verificare se almeno uno differisce. Mette a confronto la variabilità tra gruppi con la variabilità all’interno dei gruppi tramite la statistica F.

Esempio con Pingouin: confrontiamo la lunghezza delle pinne (flipper) dei pinguini tra specie diverse.

penguins = pg.read_dataset('penguins')
pg.anova(data=penguins, dv='flipper_length_mm', between='species').round(2)

Se il p-value è molto piccolo (es. 0.0 nei risultati arrotondati), possiamo rifiutare l’ipotesi nulla e concludere che la specie è un predittore significativo della lunghezza della pinna.

Post-hoc

Se ANOVA rifiuta H0, esegui test post-hoc (es. Tukey) per sapere quali gruppi differiscono.

Test non parametrici

Molti test statistici assumono una distribuzione per i dati (ad esempio normalità). Quando queste assunzioni non sono realistiche, i test non parametrici forniscono alternative robuste.

Esempi:

Mann-Whitney U: alternativa non parametrica al t-test per due gruppi indipendenti.
Kruskal-Wallis: alternativa non parametrica all’ANOVA per più gruppi.

Esempio rapido con Mann-Whitney U:

a = rng.random(15)
b = rng.random(15)
pg.mwu(a, b)

Kruskal-Wallis sui pinguini:

pg.kruskal(data=penguins, dv='flipper_length_mm', between='species').round(2)

Interpretazione: risultati simili ad ANOVA suggeriscono che specie predice la lunghezza della pinna anche senza assumere normalità.

Quando i test falliscono

I test possono portare a conclusioni errate in questi casi:

Campione troppo piccolo: bassa potenza e rischio di errore di Tipo II.
Violazione delle assunzioni: normalità, omoschedasticità, indipendenza.
Multipli confronti non corretti: aumenta il rischio di falsi positivi.
Dati selezionati post-hoc o p-hacking: analisi non pre-registrate possono distorcere i risultati.

Esempi pratici di fallimento

Un test con p-value = 0.04 su 20 variabili esplorate senza correzione potrebbe essere un falso positivo.
Serie temporali con autocorrelazione: test standard ignorando l’autocorrelazione possono dare p-value fuorvianti.

Mitigazioni

Aumentare la dimensione del campione quando possibile.
Usare test robusti o non parametrici.
Applicare correzioni per test multipli (es. Bonferroni, Benjamini–Hochberg).
Pre-registrare ipotesi e piano analitico.

Mini-metodologia passo-passo per un test di ipotesi

Definisci domanda e ipotesi H0 e H1 con chiarezza.
Scegli il test appropriato in base al tipo di variabile e alle assunzioni.
Scegli alpha (es. 0,05) e calcola la dimensione del campione necessaria, se possibile.
Esegui controlli preliminari: outlier, missing, normalità, varianze.
Applica il test e calcola p-value, statistica di test e intervalli di confidenza.
Valuta significatività statistica e rilevanza pratica (dimensione dell’effetto).
Se rilevante, esegui analisi post-hoc o test di robustezza.
Documenta e comunica risultati, includendo limiti e assunzioni.

Playbook rapido per analisi statistica in Python

Ambiente: usa un notebook Jupyter per riproducibilità.
Librerie: pandas, numpy, scipy, pingouin, statsmodels, seaborn, matplotlib.
Versionamento: salva i notebook e registra le versioni delle librerie.
Report: includi tabelle con statistiche e grafici con intervalli di confidenza.

Esempio di playbook passo per passo

Step 1: Carica dati in pandas e ispeziona con .info(), .describe(), .head().
Step 2: Pulizia: gestisci missing, filtra outlier giustificati.
Step 3: Visualizza dati con grafici esplorativi (boxplot, histogram, scatter).
Step 4: Test di assunzioni (Shapiro-Wilk per normalità, Levene per omogeneità varianze).
Step 5: Scegli il test e applicalo con Pingouin o SciPy.
Step 6: Valuta risultati, controlla robustezza.
Step 7: Redigi report con conclusioni chiare e raccomandazioni.

Checklist per ruoli

Data Scientist

Definire H0 e H1
Verificare assunzioni e dimensione del campione
Eseguire test principali e test alternativi
Fornire intervalli di confidenza e misure di effetto
Documentare codice e versioni delle librerie

Ricercatore/Clinico

Pre-registrare il piano di analisi
Giustificare la scelta del test e alpha
Assicurare adeguata potenza statistica
Valutare implicazioni etiche di errori di Tipo I/II

Product Manager/Stakeholder

Richiedere misura dell’effetto oltre al p-value
Valutare impatto pratico dei risultati
Chiedere robustezza e test A/B ben disegnati

Casi di test e criteri di accettazione

Esempio: t-test per incremento medio di conversione

Input: due gruppi A/B con almeno 1000 utenti ciascuno.
Test: t-test per campioni indipendenti (o test non parametrico se non normale).
Criterio di accettazione: p-value < 0,05 e aumento medio della metrica > soglia pratica predefinita.
Azione se non superato: non rilasciare cambiamento; analisi ulteriore o aumentare campione.

Diagramma decisionale per la scelta del test

flowchart TD
  A[Hai una variabile dipendente continua?] -->|No| B[Usa test per variabili categoriali]
  A -->|Sì| C[Hai una sola variabile indipendente categoriale?]
  C -->|Sì, 2 gruppi| D{Dati normali?}
  C -->|Sì, >2 gruppi| E{Dati normali?}
  D -->|Sì| F[T-test]
  D -->|No| G[Mann-Whitney U]
  E -->|Sì| H[ANOVA]
  E -->|No| I[Kruskal-Wallis]
  F --> J[Valuta dimensione dell'effetto]
  G --> J
  H --> K[Post-hoc se necessario]
  I --> K

Fattori chiave e numeri utili

Alpha comunemente usati: 0,05 (95% confidenza), 0,01 (99% confidenza).
Tipi di errore: Tipo I = falso positivo; Tipo II = falso negativo.
Potenza statistica: probabilità di rifiutare H0 quando H1 è vera; aumenta con la dimensione del campione.
Correzioni per confronti multipli: Bonferroni (conservativa), Benjamini–Hochberg (FDR).

Glossario sintetico

Ipotesi nulla: ipotesi di assenza di effetto.
p-value: probabilità di osservare dati almeno così estremi sotto H0.
t-value/F-value: statistiche di test che misurano quanto i dati si discostano da H0.
Intervallo di confidenza: range plausibile per un parametro con un certo livello di confidenza.

Note su privacy e dati personali

Se lavori con dati personali (es. clinici), applica misure di minimizzazione, anonimizzazione e conformità GDPR.
Evita l’esposizione di record identificabili nei notebook o nei report pubblici.

Suggerimenti per comunicare i risultati

Presenta p-value, dimensione dell’effetto e intervalli di confidenza.
Spiega limiti e assunzioni.
Indica azioni pratiche suggerite dai risultati.

Esempi di messaggi per anteprima social

Titolo OG: Test statistici in Python — guida pratica
Descrizione OG: Capire p-value, t-test, regressione e test non parametrici con esempi Python e buone pratiche.

Versione breve per annuncio (100–200 parole)

La statistica non è solo matematica: è metodo. Questa guida pratica mostra come usare Python per testare ipotesi, confrontare medie con il t-test, eseguire regressioni e applicare test non parametrici quando le assunzioni non tengono. Troverai esempi concreti con Pingouin, Seaborn e NumPy, checklist operative per ruoli diversi, e un playbook passo-passo per condurre analisi riproducibili. Pianifica sempre ipotesi e livello di significatività prima dell’analisi, controlla assunzioni e valuta la dimensione dell’effetto insieme al p-value. La guida include anche un diagramma decisionale per scegliere il test giusto e suggerimenti per comunicare i risultati in modo chiaro.

Riepilogo

Pianifica ipotesi e alpha in anticipo.
Usa test appropriati e controlla le assunzioni.
Privilegia misure di effetto e intervalli di confidenza oltre ai p-value.
Quando i dati non rispettano le assunzioni, passa a test non parametrici.

Importante

Nessun test può sostituire buon disegno sperimentale e giudizio critico. Documenta le scelte e riproduci le analisi.

Test statistici in Python: guida pratica a ipotesi, t-test, regressione e non parametrici