Операции над аудиосигналами в Octave: сложение, умножение и масштабирование

Кратко: покажем, как в Octave складывать, умножать и масштабировать аудиосигналы. Примеры включают синтез косинусоид, сложение двух дорожек, поэлементное умножение (модуляция) и умножение на скаляр. В конце — практические советы по нормализации, проверке совпадения частоты дискретизации и возможным проблемам.

Введение

В прошлом учебнике рассматривались основы чтения, записи и воспроизведения аудиофайлов и синтеза простых сигналов (например, косинусоид). Здесь мы разберём базовые математические операции над сигналами: сумму, поэлементное умножение и умножение на скаляр. Покажем графики и поясним, как эти операции влияют на временную форму и слышимый результат.

Важно: все примеры используют Octave/Matlab-подобный синтаксис. Кодовые блоки в тексте оставлены без изменений для точного воспроизведения.

Добавление сигналов

Сумма двух сигналов S1(t) и S2(t) даёт сигнал R(t), значение которого в любой момент равно сумме значений слагаемых:

R(t) = S1(t) + S2(t)

Ниже воспроизводится процесс создания двух простых косинусоид и их сложения.

Шаг 1: Создание двух сигналов разной частоты (ogg-файлы)

(код оставлен без изменений; комментарии исходного примера на английском сохранены)

>> sig1='cos440.ogg';                    %creating the audio file @440 Hz  
>> sig2='cos880.ogg';                    %creating the audio file @880 Hz  
>> fs=44100;                                     %generating the parameters values (Period, sampling frequency and angular frequency)  
>> t=0:1/fs:0.02;  
>> w1=2*pi*440*t;  
>> w2=2*pi*880*t;  
>> audiowrite(sig1,cos(w1),fs);      %writing the function cos(w) on the files created  
>> audiowrite(sig2,cos(w2),fs);

Пояснение: мы синтезируем две косинусоиды на 440 Гц и 880 Гц, записываем их в ogg и затем загружаем для отображения.

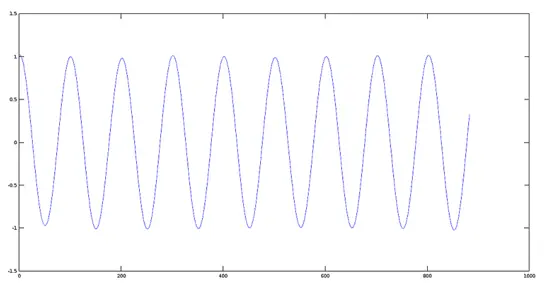
График сигнала 1 — 440 Гц

>> [y1, fs] = audioread(sig1);  
>> plot(y1)

График сигнала 2 — 880 Гц

>> [y2, fs] = audioread(sig2);  
>> plot(y2)

Шаг 2: Сложение двух сигналов

Поэлементное сложение двух векторов (одинаковой длины) даёт результирующий сигнал:

>> sumres=y1+y2;  
>> plot(sumres)

График суммы сигналов

Важно: перед сложением убедитесь, что у файлов одинаковая частота дискретизации и одинаковая длина. Если длины отличаются, усеките или заполните нулями более короткий сигнал.

Примечание по эффекту «октавера»

Эффект Octaver создаёт дополнительную ноту на нижней или верхней октаве, одновременно с оригинальным звуком. Технически это похоже на суммирование исходного сигнала с тем же сигналом, изменённым по частоте/времени.

Шаг 3: Сложение двух реальных дорожек (пример с двумя музыкальными треками)

Пример ниже показывает сложение двух файлов с вокальной семплировкой (григорианские хоралы).

Avemaria — чтение и отображение

>> [y1,fs]=audioread('avemaria_.ogg');  
>> plot(y1)

Hymnus — чтение и отображение

>> [y2,fs]=audioread('hymnus.ogg');  
>> plot(y2)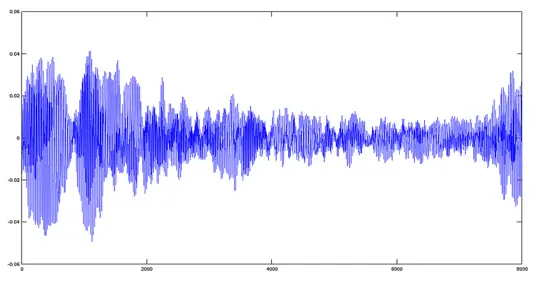

Смешивание двух дорожек

>> y='avehymnus.ogg';  
>> audiowrite(y, y1+y2, fs);  
>> [y, fs]=audioread('avehymnus.ogg');  
>> plot(y)

Аудио-практика: результат — простое суммирование дорожек; при этом суммарный уровень может превысить допустимый диапазон (клиппинг). Рекомендуется нормализовать или масштабировать уровни перед финальной записью.

Произведение двух сигналов

Поэлементное умножение двух сигналов реализуется аналогично сложению, но выполняется оператором element-wise ‘.*’ в Octave/Matlab:

R(t) = S1(t) * S2(t) (поэлементно)

Пример по тем же файлам:

>> sig1='cos440.ogg';                        %creating the audio file @440 Hz  
>> sig2='cos880.ogg';                        %creating the audio file @880 Hz  
>> product='prod.ogg';                   %creating the audio file for product  
>> fs=44100;                                      %generating the parameters values (Period, sampling frequency and angular frequency)  
>> t=0:1/fs:0.02;  
>> w1=2*pi*440*t;  
>> w2=2*pi*880*t;  
>> audiowrite(sig1, cos(w1), fs);        %writing the function cos(w) on the files created  
>> audiowrite(sig2, cos(w2), fs);  
>> [y1,fs]=audioread(sig1);  
>> [y2,fs]=audioread(sig2);  
>> audiowrite(product, y1.*y2, fs);    %performing the product  
>> [yprod,fs]=audioread(product);  
>> plot(yprod);                             %plotting the product

Обратите внимание: нужен оператор ‘.‘ — это поэлементное умножение векторов. Обычный ‘‘ — матричное умножение и для векторов не подойдёт.

График произведения двух сигналов

Принцип модуляции — сильная разность основных частот

Умножение сигнала с низкой частотой (несущая) на высокочастотный модулятор иллюстрирует базовую AM-модуляцию: получаются огибающие и новые спектральные составляющие.

Шаг 1: носитель 220 Гц

>> fs=44100;  
>> t=0:1/fs:0.03;  
>> w=2*pi*220*t;  
>> y1=cos(w);  
>> plot(y1);

Шаг 2: модулирующий сигнал 22000 Гц

>> y2=cos(100*w);  
>> plot(y2);

Шаг 3: умножение и отображение

>> plot(y1.*y2);

Аудиторно это приводит к появлению побочных спектров (боковых полос). В частотной области поэлементное умножение во временной области эквивалентно свёртке спектров исходных сигналов.

Умножение сигнала на скаляр

Умножение функции F(t) на скаляр K изменяет амплитуду и, при отрицательном K, инвертирует фазу:

R(t) = K * F(t)

Пример в Octave:

>> [y,fs]=audioread('cos440.ogg');       %creating the work files  
>> res1='coslow.ogg';                      
>> res2='coshigh.ogg';  
>> res3='cosinverted.ogg';  
>> K1=0.2;                                       %values of the scalars  
>> K2=0.5;  
>> K3=-1;  
>> audiowrite(res1, K1*y, fs);           %product function-scalar  
>> audiowrite(res2, K2*y, fs);  
>> audiowrite(res3, K3*y, fs);

График оригинального сигнала

График сигнала с амплитудой 0.2

>> plot(res1)

График сигнала с амплитудой 0.5

>> plot(res2)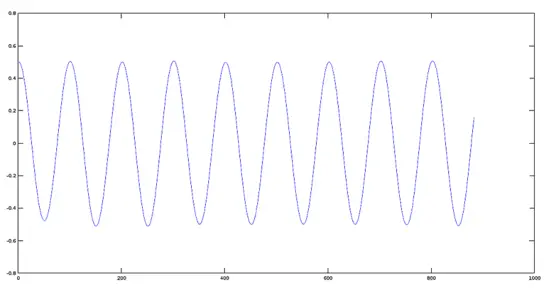

График сигнала с инвертированной фазой

>> plot(res3)

Практические советы и распространённые ошибки

Важно: всегда проверяйте совпадение fs (частоты дискретизации) у всех файлов перед операцией. Разная fs приведёт к неверным результатам.

• Совпадение длины: для поэлементных операций длины векторов должны совпадать. Усечение или padding нулями — стандартные способы выровнять длины.
• Нормализация: после сложения или умножения возможно превышение диапазона [-1, 1] для плавающей записи — применяется нормализация или компрессия, чтобы избежать клиппинга.
• Антиалиасинг: при создании высокочастотных модулей следите за теоремой Найквиста (fs/2). Модулирующий сигнал 22000 Гц при fs=44100 близок к верхнему пределу и может давать искажения.
• Тип умножения: используйте ‘.‘ для поэлементных операций. Операторы ‘‘ и ‘/‘ предназначены для матриц.

Когда метод не работает или даёт неожиданный результат

• Сигналы разной fs: при чтении двух файлов с разной частотой дискретизации прямое сложение недопустимо.
• Разная длина: если не выровнять длины, Octave выдаст ошибку или выполнит автотрансляцию (если формы совместимы), что может привести к неверным данным.
• Клиппинг: суммарная амплитуда превышает допустимый диапазон — слышимые искажения.
• Алиасинг: при работе с компонентами выше fs/2 появляются артефакты.

Альтернативные подходы и расширения

• Работать в частотной области: вместо умножения во временной области используйте FFT — умножение в частотной области эквивалентно свёртке во временной и наоборот. Это полезно для фильтрации и точечной модификации спектра.
• Использовать оконные функции и перекрытия при обработке длинных сигналов (STFT) для локальных преобразований.
• Для реалистичного микширования треков применять нормализацию LUFS/компрессию вместо простого масштабирования амплитуды.

Мини-методология: быстрый чеклист для эксперимента

1. Убедиться, что fs одинаковый у всех файлов.
2. Выровнять длины (усечь или дополнить нулями).
3. Выполнить операцию (сложение/умножение/масштаб).
4. Построить график и прослушать результат на малой громкости.
5. Нормализовать / применить лимитер, если есть клиппинг.
6. Сохранить итоговый файл.

Критерии приёмки

• Итоговый файл не содержит клиппинга при нормальном уровне воспроизведения.
• Сохранены временные соотношения сигналов (нет неожиданной деформации во времени).
• Частота дискретизации в выходном файле соответствует ожидаемой (fs).

Краткий глоссарий

• fs — частота дискретизации (sample rate).
• Носитель (carrier) — несущая сигнала при модуляции.
• Модулятор — сигнал, который изменяет носитель по амплитуде или фазе.
• Клиппинг — искажение при превышении допустимого амплитудного диапазона.
• Aliasing — наложение спектральных компонентов выше fs/2.

Итог

Базовые операции — сложение, поэлементное умножение и масштабирование — лежат в основе многих DSP-приёмов: смешивание, амплитудная модуляция, свёртка/фильтрация и подготовка сигналов для анализа. Всегда проверяйте частоту дискретизации и амплитудный диапазон, нормализуйте результат и слушайте итог на разной громкости.

Примечание: в следующем уроке будет подробно показано, как применять эти операции в частотной области (FFT), а также использование амплитудной и фазовой модуляции для создания эффектов.