Operazioni matematiche sui segnali audio con Octave

Introduzione

Nel tutorial precedente abbiamo visto come leggere, scrivere e riprodurre file audio e come sintetizzare un segnale periodico (ad esempio una cosenoide). Qui vedremo tre operazioni fondamentali sulle forme d’onda:

• somma di segnali (mixing)
• prodotto punto-a-punto (modulazione e prodotti non lineari)
• moltiplicazione per scalare (controllo dell’ampiezza e inversione di fase)

Queste operazioni sono la base per tecniche più avanzate come analisi spettrale, modulazione di ampiezza e modulazione angolare.

Varianti d’intento (parole chiave correlate)

• sommare segnali audio
• modulazione in ampiezza
• prodotto di segnali in Octave
• scalare ampiezza segnale

A cosa servono queste operazioni (breve definizione)

Somma: combina due segnali nel dominio del tempo per ottenere un mix.
Prodotto: moltiplica valore per valore; è usato per modulazione e per introdurre componenti in banda laterale.
Moltiplicazione per scalare: cambia l’ampiezza e può invertire la fase.

Importante: tutte le operazioni mostrate sono punto-a-punto; per operazioni nel dominio della frequenza (filtraggio, convoluzione) servono metodi aggiuntivi come FFT e filtri digitali.

Aggiunta di segnali

La somma di due segnali S1(t) e S2(t) è un segnale R(t) il cui valore in ogni istante è la somma dei valori dei segnali originali in quell’istante:

R(t) = S1(t) + S2(t)

Nel seguito ricreeremo la somma in Octave e mostreremo l’effetto graficamente. Genereremo due segnali sinusoidali di diversa frequenza per osservare la forma risultante.

Passo 1: Creare due segnali di frequenze diverse (file .ogg)

>> sig1='cos440.ogg';                   %creating the audio file @440 Hz  
>> sig2='cos880.ogg';                   %creating the audio file @880 Hz  
>> fs=44100;                            %generating the parameters values (Period, sampling frequency and angular frequency)  
>> t=0:1/fs:0.02;  
>> w1=2*pi*440*t;  
>> w2=2*pi*880*t;  
>> audiowrite(sig1,cos(w1),fs);        %writing the function cos(w) on the files created  
>> audiowrite(sig2,cos(w2),fs);

Qui andremo a plottare entrambi i segnali.

Grafico del segnale 1 (440 Hz)

>> [y1, fs] = audioread(sig1);  
>> plot(y1)

Grafico del segnale 2 (880 Hz)

>> [y2, fs] = audioread(sig2);  
>> plot(y2)

Passo 2: Sommare i due segnali

>> sumres=y1+y2;  
>> plot(sumres)

Osservazioni: quando si sommano due cosenoidi di frequenza diversa si ottiene una forma risultato che contiene entrambe le componenti; in audio si ascolta un suono con armoniche multiple o battimenti a seconda della relazione tra le frequenze.

Effetto Octaver

Un effetto octaver riproduce la nota suonata in un’ottava inferiore o superiore (a seconda della programmazione) contemporaneamente al suono originale. In pratica si ottengono due note percepite insieme, che possono rendere il suono più pieno o creare timbri particolari.

Passo 3: Sommare segnali reali (esempio con due tracce musicali)

Useremo due tracce di canto gregoriano per mostrare la somma di segnali reali.

Grafico della traccia Avemaria:

>> [y1,fs]=audioread('avemaria_.ogg');  
>> plot(y1)

Grafico della traccia Hymnus:

>> [y2,fs]=audioread('hymnus.ogg');  
>> plot(y2)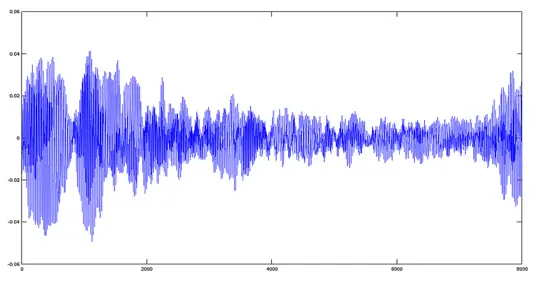

Somma e scrittura su file:

>> y='avehymnus.ogg';  
>> audiowrite(y, y1+y2, fs);  
>> [y, fs]=audioread('avehymnus.ogg');  
>> plot(y)

Il risultato è un mix: da un punto di vista uditivo si percepiscono entrambe le tracce sovrapposte.

Prodotto di due segnali

Per moltiplicare due segnali si procede in modo analogo alla somma, ma usando il prodotto punto-a-punto. Il prodotto può essere usato per modulazione o per generare componenti spettrali diverse.

R(t) = S1(t) * S2(t)

Esempio con i file precedenti:

>> sig1='cos440.ogg';                   %creating the audio file @440 Hz  
>> sig2='cos880.ogg';                   %creating the audio file @880 Hz  
>> product='prod.ogg';                  %creating the audio file for product  
>> fs=44100;                            %generating the parameters values (Period, sampling frequency and angular frequency)  
>> t=0:1/fs:0.02;  
>> w1=2*pi*440*t;  
>> w2=2*pi*880*t;  
>> audiowrite(sig1, cos(w1), fs);      %writing the function cos(w) on the files created  
>> audiowrite(sig2, cos(w2), fs);  
>> [y1,fs]=audioread(sig1);  
>> [y2,fs]=audioread(sig2);  
>> audiowrite(product, y1.*y2, fs);    %performing the product  
>> [yprod,fs]=audioread(product);  
>> plot(yprod);                        %plotting the product

Nota: è necessario usare l’operatore ‘.*’ perché il prodotto è eseguito elemento per elemento tra i vettori. Per dettagli sulle operazioni con matrici, consultare il manuale di Octave.

Grafico del segnale prodotto

Effetto grafico della moltiplicazione quando le frequenze fondamentali sono molto diverse (principi di modulazione)

Creiamo un segnale portante a 220 Hz e un modulante ad una frequenza molto più alta per vedere l’effetto di modulazione.

Passo 1 — portante 220 Hz:

>> fs=44100;  
>> t=0:1/fs:0.03;  
>> w=2*pi*220*t;  
>> y1=cos(w);  
>> plot(y1);

Passo 2 — modulante a 22 kHz (100× la portante nel codice d’esempio):

>> y2=cos(100*w);  
>> plot(y2);

Passo 3 — moltiplicazione e grafico:

>> plot(y1.*y2);

Osservazione: il prodotto genera componenti a frequenze somma e differenza: questo è il principio base della modulazione di ampiezza.

Moltiplicare un segnale per uno scalare

Moltiplicare un segnale per uno scalare K equivale a modificare l’ampiezza (e, se K è negativo, la fase). Dato K si definisce:

R(t) = K * F(t)

Esempio pratico:

>> [y,fs]=audioread('cos440.ogg');         %creating the work files  
>> res1='coslow.ogg';                     
>> res2='coshigh.ogg';  
>> res3='cosinverted.ogg';  
>> K1=0.2;                                %values of the scalars  
>> K2=0.5;  
>> K3=-1;  
>> audiowrite(res1, K1*y, fs);            %product function-scalar  
>> audiowrite(res2, K2*y, fs);  
>> audiowrite(res3, K3*y, fs);

Grafico del segnale originale:

>> plot(y)

Grafico segnale ridotto in ampiezza (K=0.2):

>> plot(res1)

Grafico segnale ridotto in ampiezza (K=0.5):

>> plot(res2)

Grafico segnale invertito in fase (K=-1):

>> plot(res3)

Quando queste operazioni possono fallire o risultare fuorvianti

• Differente lunghezza dei segnali: somma o prodotto richiedono vettori della stessa lunghezza. Se non lo sono, normalizzare o ritagliare.
• Overflow/clipping: sommare segnali ad alta ampiezza può superare il range [-1,1] per file audio float; applicare normalizzazione o limitazione (clipping) intenzionale.
• Alias: lavorare con frequenze vicine a Nyquist (fs/2) senza filtraggio provoca aliasing; attenzione alla scelta di fs.
• Interpretazione spettrale: la somma è lineare; il prodotto introduce intermodulazioni che complicano l’analisi nello spettro.

Approcci alternativi

• Lavorare nel dominio della frequenza (FFT) per manipolare bande specifiche e poi tornare al dominio tempo con IFFT.
• Utilizzare convoluzione per effetti lineari (filtri, riverberi) invece della moltiplicazione diretta.
• Usare librerie audio dedicate (librosa in Python, SoX, Audacity scripting) per workflow più complessi.

Mini-metodologia rapida (checklist operativa)

1. Verifica fs e durata dei file (audioread).
2. Allinea durate: ritaglia o campiona.
3. Applica operazione: y_sum = y1 + y2, y_prod = y1 . y2, y_scaled = Ky.
4. Normalizza se necessario prima di scrivere su file: y = y / max(abs(y)).
5. Ascolta e controlla il grafico e lo spettro (plot e fft).

Scheda numerica chiave

• Frequenza di campionamento esempio: 44100 Hz
• Durata esempi: 0.02–0.03 s
• Moltiplicatore modulazione nell’esempio: 100× la frequenza della portante
• Range tipico segnale audio (floating point normalizzato): [-1, 1]

Cheat sheet / Comandi utili in Octave

• Leggere file: [y, fs] = audioread(‘file.ogg’)
• Scrivere file: audiowrite(‘out.ogg’, y, fs)
• Sommare: y = y1 + y2
• Prodotto elemento per elemento: y = y1 .* y2
• Scalare: y = K * y
• Normalizzare: y = y / max(abs(y))
• Plot: plot(y); xlabel(‘campioni’); ylabel(‘ampiezza’)

Checklist per ruolo

• Studente: verifica lunghezza vettori, visualizza grafici, ascolta prima e dopo.
• Ingegnere audio: controlla clip, applica normalizzazione e filtri antialiasing.
• Musicista/Producer: usa automazioni di gain e crossfade per evitare tagli bruschi.

Conclusione

Le operazioni matematiche di base — somma, prodotto e moltiplicazione per scalare — sono fondamentali per il trattamento del suono. Consentono di costruire effetti come mix, modulazione in ampiezza e controllo dinamico. Nel prossimo tutorial esploreremo l’analisi spettrale (FFT) e le tecniche di modulazione più avanzate.

Note finali: quando applichi queste operazioni, presta attenzione a durata, frequenza di campionamento e normalizzazione per evitare artefatti udibili.