Opérations mathématiques de base sur des signaux audio avec Octave

Introduction

Dans le tutoriel précédent, nous avons vu comment lire, écrire et reproduire des fichiers audio. Nous avons aussi synthétisé un fichier audio à partir d’une fonction périodique (cosinus). Ici, nous appliquons des opérations mathématiques élémentaires aux signaux : addition, multiplication (modulation) et multiplication par un scalaire. Nous observons leur effet sur le signal d’origine, à l’aide d’exemples Octave et de tracés.

Important — Définitions rapides

• Signal : une suite de valeurs représentées en fonction du temps.
• Échantillonnage (fs) : nombre d’échantillons par seconde, ex. 44100 Hz.

Addition de signaux

La somme de deux signaux S1(t) et S2(t) donne un signal R(t) tel que R(t) = S1(t) + S2(t). Cette opération s’effectue valeur par valeur (échantillon par échantillon). Nous recréons cette somme dans Octave et observons le résultat graphiquement.

Étape 1 : Création de deux signaux de fréquences différentes (fichiers .ogg)

>> sig1='cos440.ogg';            % créer le fichier audio @440 Hz
>> sig2='cos880.ogg';            % créer le fichier audio @880 Hz
>> fs=44100;                     % fréquence d'échantillonnage
>> t=0:1/fs:0.02;
>> w1=2*pi*440*t;
>> w2=2*pi*880*t;
>> audiowrite(sig1,cos(w1),fs);  % écrire cos(w1) dans sig1
>> audiowrite(sig2,cos(w2),fs);

Voici les tracés des deux signaux.

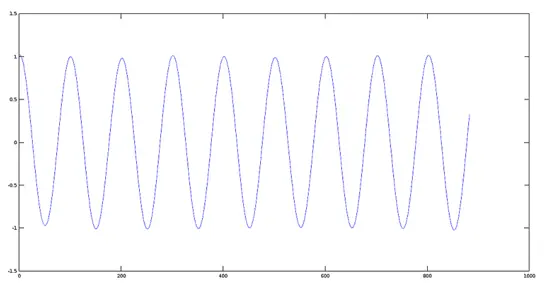
Tracé du signal 1 (440 Hz)

>> [y1, fs] = audioread(sig1);
>> plot(y1)

Tracé du signal 2 (880 Hz)

>> [y2, fs] = audioread(sig2);
>> plot(y2)

Étape 2 : Additionner les deux signaux

>> sumres = y1 + y2;
>> plot(sumres)

Note — Lorsque vous additionnez des sinusoïdes, vous obtenez une nouvelle forme d’onde. Si les signaux ont des phases ou amplitudes différentes, il peut y avoir annulation partielle (interférence destructive) ou renforcement (interférence constructive).

Exemple concret : ajout de deux pistes réelles (chant grégorien)

Nous utilisons deux pistes vocales pour démontrer le mixage par addition.

Piste Avemaria

>> [y1,fs] = audioread('avemaria_.ogg');
>> plot(y1)

Piste Hymnus

>> [y2,fs] = audioread('hymnus.ogg');
>> plot(y2)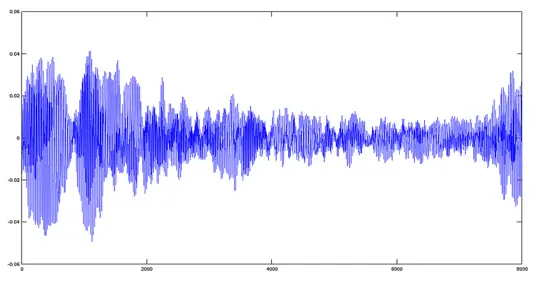

Avemaria + Hymnus

>> y='avehymnus.ogg';
>> audiowrite(y, y1 + y2, fs);
>> [y, fs] = audioread('avehymnus.ogg');
>> plot(y)

Remarque pratique — Le simple ajout peut provoquer une saturation/clipping si la somme dépasse la plage d’échantillonage. Normalisez ou atténuez avant d’écrire le fichier.

Produit de deux signaux

Le produit point par point de deux signaux s’effectue avec l’opérateur élémentaire ‘.‘ en Octave. Mathématiquement R(t) = S1(t) S2(t). Cette opération est utilisée pour la modulation d’amplitude et la détection.

>> sig1='cos440.ogg';
>> sig2='cos880.ogg';
>> product='prod.ogg';
>> fs=44100;
>> t=0:1/fs:0.02;
>> w1=2*pi*440*t;
>> w2=2*pi*880*t;
>> audiowrite(sig1, cos(w1), fs);
>> audiowrite(sig2, cos(w2), fs);
>> [y1,fs]=audioread(sig1);
>> [y2,fs]=audioread(sig2);
>> audiowrite(product, y1 .* y2, fs);  % produit échantillon par échantillon
>> [yprod,fs]=audioread(product);
>> plot(yprod);

Note — Utilisez ‘.*’ pour indiquer un produit élément par élément. Le produit de sinusoïdes crée des composantes à la somme et à la différence des fréquences (théorème d’identité trigonométrique), d’où l’intérêt en modulation.

Tracé du produit

Modulation (principe : grande différence de fréquence)

Exemple pas à pas pour illustrer la modulation d’amplitude graphique.

Étape 1 — Porteuse à 220 Hz

>> fs=44100;
>> t=0:1/fs:0.03;
>> w=2*pi*220*t;
>> y1=cos(w);
>> plot(y1);

Étape 2 — Modulante à fréquence élevée (ex. 22000 Hz)

>> y2 = cos(100 * w);
>> plot(y2);

Étape 3 — Multiplication (modulation)

>> plot(y1 .* y2);

Interprétation — Le produit met en évidence des composantes spectrales décalées (bandes latérales). En audio numérique, la qualité dépendra du respect du théorème de Nyquist et de l’absence d’aliasing.

Multiplication par un scalaire

Multiplier un signal par un scalaire K change son amplitude et peut inverser sa phase si K est négatif : R(t) = K * F(t).

>> [y,fs] = audioread('cos440.ogg');
>> res1='coslow.ogg';
>> res2='coshigh.ogg';
>> res3='cosinverted.ogg';
>> K1 = 0.2;
>> K2 = 0.5;
>> K3 = -1;
>> audiowrite(res1, K1 * y, fs);
>> audiowrite(res2, K2 * y, fs);
>> audiowrite(res3, K3 * y, fs);

Tracés :

Signal original

Signal réduit (amplitude ×0.2)

Signal réduit (amplitude ×0.5)

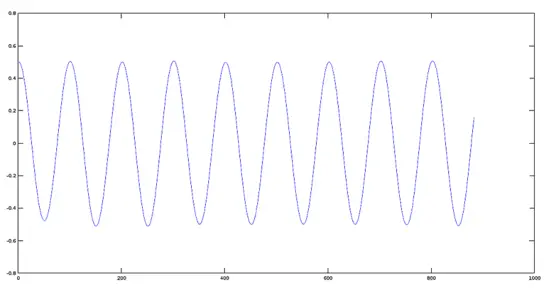
Signal avec inversion de phase (×-1)

Pratique — Pour préserver la dynamique, normalisez après multiplication si vous prévoyez d’exporter vers des formats limités (ex. 16 bits PCM).

Fact box — paramètres clés

• Fréquence d’échantillonnage courante : 44100 Hz
• Opération d’addition : somme échantillon par échantillon
• Opération de produit : ‘.*’ en Octave pour produit point par point
• Risque principal : saturation/clipping lorsque les amplitudes dépassent la plage

Contre-exemples et limites

• Addition sans mise à l’échelle peut saturer un mixage stéréo. Toujours vérifier le niveau maximal.
• Multiplication non filtrée entre fréquences proches peut générer battements indésirables.
• Modulation à la fréquence d’échantillonnage/2 provoque de l’aliasing si non filtrée.

Approches alternatives

• Mixage professionnel : utilisez un bus somme et appliquez des réductions de gain (gain staging) avant sommation.
• Modulation analogique simulée : appliquez des filtres passe-bande avant et après la modulation.
• Convolution ou traitement en domaine fréquentiel pour opérations complexes.

Mini-méthodologie : procédure sûre pour additionner deux pistes

1. Charger les deux pistes et vérifier fs identique.
2. S’assurer que les pistes ont la même longueur (padding ou découpe).
3. Attribuer un gain d’inspection (-6 dB par piste recommandé) pour éviter la saturation.
4. Somme échantillon par échantillon.
5. Normaliser ou limiter si nécessaire.
6. Écouter en mono pour détecter annulations de phase.

Checklist par rôle

• Ingénieur du son : vérifier phase, appliquer égalisation, contrôler la dynamique.
• Chercheur audio : documenter fs, durée, windowing si utilisé en FFT.
• Étudiant : tracer formes d’onde et spectres pour comprendre effets.

Tests et critères de succès

• Le fichier exporté ne présente pas d’écrêtage (aucun échantillon à ±1 en flottant ou ±32767 en 16 bits).
• L’opération respecte la durée et la fréquence d’échantillonnage initiales.
• Visuellement, le tracé correspond aux attentes (interférences visibles pour l’addition, enveloppe pour la modulation).

Glossaire (1 ligne)

• Nyquist : fréquence maximale représentable = fs/2.

Diagramme de décision (choisir l’opération)

flowchart TD
  A[Début] --> B{Voulez-vous combiner deux signaux?}
  B -- Oui --> C{Voulez-vous mélanger ou moduler?}
  C -- Mélanger --> D[Additioner 'y1+y2' puis normaliser]
  C -- Moduler --> E[Multiplier 'y1.*y2' puis filtrer]
  B -- Non --> F[Appliquer un scalaire K*signal]
  D --> G[Contrôler clipping]
  E --> G
  F --> G
  G --> H[Exporter]

Résumé

Les opérations de base — addition, produit et mise à l’échelle — permettent d’explorer des traitements plus avancés (analyse spectrale, modulation en amplitude, etc.). En pratique, surveillez toujours les niveaux pour éviter la saturation et considérez le filtrage pour prévenir l’aliasing lors des opérations de modulation.

Notes — Dans le prochain tutoriel, nous verrons l’analyse spectrale et les effets de ces opérations dans le domaine fréquentiel.